TURÁN PÁL (Budapest, 1910. aug. 18. - Budapest, 1976. szept. 26.)

Már diákkorában kitűnt matematikai tehetségével mint a Középiskolai Matematikai és Fizikai Lapok egyik kiemelkedő feladatmegoldója. 1933-ban matematika-fizika tanári diplomát szerzett a budapesti Tudományegyetemen, 1935-ben doktorált Fejér Lipótnál. Jelentős tudományos eredményei ellenére nem kapott tanári állást. Diákokat korrepetált 1938-ig, amikor helyettes tanárként alkalmazta a budapesti izraelita gimnázium. A háború alatt munkaszolgálatra hívták be, de ő a legsúlyosabb helyzetekben sem hagyott fel matematikai kutatómunkájával, több jelentős eredményét munkaszolgálatos korában fedezte fel. 1945-ben magántanárrá habilitálták, 1949-ben az ELTE professzora lett mint az algebrai és számelméleti tanszék vezetője. Közel harminc évig oktatott ezen az egyetemen. 1956-tól az MTA Matematikai Kutató Intézet komplex függvénytani osztályának is vezetője volt. A Magyar Tudományos Akadémia 1948-ban lev., 1953-ban r. tagjává választotta. 1945-ben és 1952-ben Kossuth-díjjal tüntették ki, 1975-ben a Bolyai János Matematikai Társulat Szele Tibor-emlékdíjban részesítette. Legjelentősebb nemzetközi elismerései közé tartozik az, hogy 1970-ben a Nemzetközi Matematikai Unió (IMU) Nizzában tartott kongresszusa alkalmával meghívták a Fields-érmet odaítélő bizottságba. Számos magyar munkatársa és tanítványa kutatott irányításával, de hónapokat töltöttek mellette Budapesten Svédországból, Hollandiából, Lengyelországból és Japánból jött fiatal kutatók is, akik részben vele együtt dolgoztak, részben vezetésével írták doktori értekezésüket. Oktatói és kutatói tevékenységén kívül számos tisztséget töltött be a matematikai közéletben, és részt vett matematikai folyóiratok szerkesztésében.

Tudományos munkásságát a sokoldalúság jellemzi, bár a számelmélet állt érdeklődésének középpontjában; 245 önállóan vagy társszerzővel írt dolgozata közül több mint 100-nak számelmélet a tárgya.

Élete fő műve, amelyben híres hatványösszeg módszerét fejti ki: Az analízis új módszeréről és annak alkalmazásairól című könyve; megjelent magyarul és németül 1953-ban, 1956-ban kínai kiadásban. Több mint húsz éven át dolgozott az angol nyelvű változat előkészítésén, de ennek megjelenését már nem érte meg. Hátrahagyott kéziratai, feljegyzései alapján azt tanítványai, Halász Gábor és Pintz János rendezték sajtó alá. Címe: On a new method of analysis and its applications (Wiley, New York, 1984.). A módszert elsősorban a számelméletben használta fel, a híres Riemann-sejtéssel kapcsolatos vizsgálataiban, majd később az összehasonlító prímszámelméletben, de alkalmazta módszerét differenciálegyenletek stabilitási és oszcillatorikus viselkedésének, valamint megoldásaik értékeloszlásainak tanulmányozására is.

Érdekes eredményekre jutott algebrai egyenletek megoldásával kapcsolatban is. Mindig eredeti problémák felvetésére, járatlan utak kipróbálására törekedett. Egyik első dolgozatában is, amelyben ismert tételre adott új bizonyítást, módszere az, ami igen fontosnak bizonyult, mert ez volt a valószínűségszámítási módszerek első alkalmazása a számelméletben. Fejér tanítványaként számos dolgozatában foglalkozott az analízis kérdéseivel. Erdős Pállal együtt több cikket írt a Lagrange-féle interpolációról és a racionális approximációról. Híres a Legendre-féle polinomokra vonatkozó Turán-féle egyenlőtlenség:

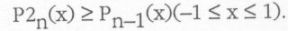
A komplex függvénytanban bebizonyította, hogy hatványsorok lokális kerületi konvergenciája nem konform invariáns. Erdős Pállal együtt kezdeményezője volt a statisztikus csoportelmélet kidolgozásának. Sokat idézik a Turán-féle gráfelméleti tételt.