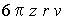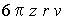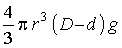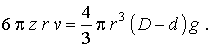Forrás: Középiskolai Mathematikai és Fizikai Lapok II.éf. 4. sz.
Az atomok világában.
(Ötödik közlemény.)
Miután a legutolsó közleményben ismertettem a Perrin-féle módszer gondolatmenetét és elméleti
megalapozását, most be fogom mutatni miként hajtotta végre a tényleges méréseket. Tulajdonképen
2 kérdésre kellett felelnie:
- milyen magasságban csökken felére a szuszpenzióban lebegő részecskék száma?
- milyen nagyok a szuszpendált szemcsék.
Mindenekelőtt azonban egy harmadik, nem kevésbbé érdekes kérdés merül fel, az, hogy miképen
állította elő a szükséges kolloid oldatokat.*) A közönséges oldatokkal
(vasoxid s. i. t.) való kísérletek nem vezettek eredményre. Végre hosszabb próbálgatás után gyantákkal
kezdett kísérletezni, amelyek közül kettő vált be. Egyik a közönségesen ismert gummigutta, sárgászöld
festék, amelyet a diákok térképek festésére szoktak használni, a másik pedig a kevésbbé ismert mastix.
Különösen egyszerű a gummigutta emulzió elkészítése. Vízbe tesszük és ujjaink között dörzsöljük. A
nyert sárgászöld folyadék már kész emulzió, és ha mikroszkópon át nézzük, csak úgy hemzseg az apró
üvegszerű gömböcskéktől. A mastix emulziót pedig úgy állítjuk elő (különben a gummiguttát is lehet így
előállítani), hogy egy darabot feloldunk alkoholban és azután az oldatot vízzel erősen felhígítjuk. A híg
oldatból a mastix rendkívül apró átlátszó üvegszerű gömböcskék alakjában kicsapódik és tejszerű
emulziót ad.
A szemcsék azonban igen különböző nagyságúak, holott nekünk olyan oldatra van szükségünk,
amelyben a részecskék egyenlők. A módszer, amellyel ezt elérhetjük, a frakcionált centrifugálás. Az
oldatot betesszük a centrifugális gépbe: a szemcsék lecentrifugálódnak és az edény fenekén iszapot
adnak. Az iszap fölötti piszkos sárgás folyadékot leöntjük és az iszapot desztillált vízben felhígítjuk,
mindaddig, míg a szemcseközi folyadék tiszta víz nem lesz. Ha az oldat már elég tiszta, megkezdjük
a frakcionálást. Legelőször a legnagyobb szemcsék csapódnak le, úgy hogy gyakran megismételt
centrifugálás által végre megkapjuk a kívánt egyenlő szemcséjű oldatot. Természetesen az eljárás
nagyon hosszadalmas. Perrin percenként 2500 fordulatszámú centrifugálissal dolgozott és csak
hónapokig tartó munka után tudott megfelelő oldatot előállítani, amikor is az 1 kg.
feldolgozott gummiguttából mindössze csak 1-2 decigramm maradt.
Most következik a szemcsék megszámlálása a különböző magasságú rétegekben. Veszünk egy 0.1 mm.
mélységű Zeiss-féle küvettát és beleteszünk egy cseppet az oldatból, ráhelyezzük a fedőlemezt és fölibe
állítjuk a mikroszkópot. A mikroszkóp beállítása nagyon éles, úgy hogy mindenik helyzetben kb. 1 µ
vastagságú réteg szemcséit mutatja, és így könnyen beállítható a különböző magasságokba. Az észlelést
azonban nagyon megnehezíti az a körülmény, hogy az észlelt szemcsék állandó mozgásban vannak. Ez a
mozgás oly elképzelhetetlenül élénk és oly sok szemcse van egyszerre a látómezőben, hogy az észlelés
teljesen lehetetlen. Legegyszerűbb volna pillanatfelvételeket készíteni, azonban a részek oly kicsinyek,
hogy a felvételek általában véve ritkán sikerülnek. Ezért Perrin egy új, igen szellemes számlálási módot
gondolt ki. A mikroszkóp szemlencséje elé beállított egy darabka aranypapírost és abba finom tűvel igen
kis lyukat fúrt. Ily módon a látómezőt annyira megszűkítette, hogy egyszerre soha sem jelentkezett 6-nál
több szemcse, és így a szem egy pillanat alatt fel tudta fogni az egész jelenséget. Most még alkalmazott
egy szabályozható elsötétítő készüléket és így egyenlő időközökben meg tudta számlálni a lyukon át
feltűnő szemcséket. Nyilvánvaló, hogy pl. 500 ily észlelet megfelel oly pillanatfölvételnek, amelynek
látómezeje 500-szor nagyobb.
Ha már most megfigyeljük az emulziót, azt találjuk, hogy rögtön a készítés után a szemcsék száma minden
magasságban egyenlő. Ha azonban az oldatot állni hagyjuk, rövid idő mulya a felsőbb rétegekben ritkulás
mutatkozik és mintegy 3 óra mulva végleges egyensúlyú helyzet áll elő. A 100 µ mélységű
küvettában Perrin a következő mélységekre állította be mikroszkópját:
5 µ, 35 µ, 65 µ, 95 µ.
Megszámlált 13000 szemcsét és azt találta, hogy a koncentrációk aránya:
100: 47: 22.6: 12
ami nagyon közel áll a következő geometriai sorhoz:
100, 48, 23, 11.1.
Egy másik kísérletsorozatnál 0.52 µ sugarú mastixszemcsékkel dolgozott. 4 fényképfelvételt
készített egymástól 6 µ távolságban fekvő rétegekről. A szemcsék megszámlálása a következő
adatokhoz vezetett:
1880, 940, 530, 305,
amely számok közel állanak a következő geometriai sorhoz:
1880, 995, 528, 280.
Vagyis a kísérletek valóban igazolják a feltevéseket, a kolloid oldat oly atmoszférának tekinthető,
amelynek óriási molekulái a mikroszkópban láthatók és megmérhetők. És ez utolsó számsor adataiból
kiviláglik, hogy annak a magasságnak, amelyben a szemcsék száma a felére csökken, a nagyságrendje
6 µ.
Ha tehát módot találunk a szemcsék nagyságának direkt meghatározására, minden szükséges adatnak
birtokába jutunk. Itt természetesen két föladattal állunk szemben: meg kell határoznunk 1. a szemcsék
sugarát, 2. a szemcséket alkotó anyag sűrűségét.
Első tekintetre azt lehetne gondolni, hogy a szemcsék nagysága áteső fényben könnyen megmérhető.
Ha azonban meggondoljuk, hogy mily kicsinyek a szemcsék, azonnal beláthatjuk, hogy a mérés nem
vezethet helyes eredményekre, nem, mert a nagyon kicsiny tárgyaknál a fényelhajlás nem hanyagolható
többé el. Ennek következtében más eljárásmódokhoz kellett folyamodni, sőt többféle módszert kellett
kigondolni, a méretek eredményeit összevetni és középértékeket venni.
Perrin módszerei közül e helyen kettőt akarok bemutatni. 1. Veszünk egy csepp nagyon híg emulziót,
rátesszük a mikroszkóp tárgylemezére, de nem födjük be, hanem engedjük lassan lepárologni. A
szemcsék rárakodnak a lemezre, és azt egyrétegű golyósorral vonják be. A mikroszkóp alatt nagyon
jól ellenőrizhetjük, hogy a szemcsék sugarai egyenlők-e és közvetlenül megszámlálhatjuk, hogy hány
szemcse esik egy adott hosszúságra, vagy pedig egy adott területre, amiből az egyes szemcsék méretei
könnyen kiszámíthatók.
2. A Stokes-féle törvény alapján. Ellenálló közegben az esés bizonyos idő mulva egyenletesen megy
végbe, a sebesség növekedésével u.i. a súrlódás is növekszik, úgy, hogy végül a sebesség akkora,
hogy a súrlódás egyenlő lesz az eső test súlyával, mikor is a sebesség nem növekedik tovább. Mármost
Stokes megállapította, hogy a súrlódás következtében fellépő ellenállás kicsiny testeknél:
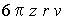
ahol z a belső súrlódás együtthatója, r az eső gömb sugara, v pedig az esés
sebessége. Viszont a testet lefelé hajtja a relatív súly
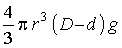
ahol D a test sűrűsége, d a folyadék sűrűsége, g pedig a nehézség gyorsulása.
Fennáll tehát a következő egyenlet:
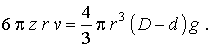
A belső súrlódás együtthatója z ismeretes, így tehát egyszerű összefüggést nyertünk r és v
között. Azonban a v nagyon könnyen megfigyelhető. Ha ugyanis a frissen készült emulziót magára
hagyjuk, megindul a folyadék tisztulása, a részecskék lefelé szállnak s a folyadékban látni lehet, mint száll
lefelé az emulziófelhő. A leszállás sebessége nagyon könnyen megállapítható (nehány mm. naponként) és ez
egyúttal az eső golyócskák sebessége, illetve annak középértéke.
A különböző mérési módszerek pontosan ugyanarra az eredményre vezettek. Perrin emulzióinak
sugarai 0.14 µ-től 0.50 µ-ig változtak.
A sűrűség megmérése nem okoz különös nehézséget. Egyszerűen alkalmazzuk a közönséges
piknometrikus eljárást. Ugyanazt az edényt megtöltjük egyszer vízzel, egyszer pedig emulzióval és
mindkétszer megmérjük a súlyt, majd beszárítjuk az emulziót és megmérjük a beszáradás után
visszamaradó üvegszerű anyag súlyát. Vagy eljárhatunk úgy is, hogy ennek az üvegszerű anyagnak
határozzuk meg a sűrűségét.
Ily módon tehát ismerjük az emulzió szemcsék méreteit, tömegét, számát az egyes rétegekben, a
ritkulás törvényét ill. azt a magasságot, amelynél a szemcsék száma a felére csökken. Minden adatunk
megvan és csak következmények levonása marad hátra.
Előre kell bocsátanom, hogy Perrin módszerének rendkívüli előnye az, hogy a mérésnél szereplő
mennyiségeket igen tág határok között változtatta. A szemcsék térfogatának változási határa 1 : 50 volt.
Változtatta a szuszpenzió anyagát (gummigutta, masztiksz), a szemcseközti folyadékot (víz, glicerin), a
szemcsék relatív súlyát, a hőmérsékletet és a viszkozitást. És a mérések mégis mindig ugyanarra az
eredményre vezettek, világos bizonyságául annak, hogy az alapföltevés helyes volt. Sőt, ami még
fontosabb, az eredmények nem különböztek lényegesen a kinetikus gázelmélet alapján nyert értékektől,
az egész eltérés alig tesz ki többet 10%-nál.
A legpontosabb mérések alapján a molekuláris méretekre nézve a következő adatokat nyerjük (Perrin).
A hidrogénatom tömege grammokban:
h = 1.47 · 10-24
A molekulák haladó mozgásának kinetikus energiája 0° mellett középértékben:
0.5 · 10-13 erg.
A szabad úthossz pl. a 370°-os higanygőzöknél:
L = 2.1 · 10-5 cm.
A molekulák átmérője millimikronokban:
| Egyatomúak | Többatomúak |
| Helium | 0.17 |
Hidrogén | 0.21 |
| Argon | 0.28 |
Oxigén | 0.28 |
| Higany | 0.29 |
Nitrogén | 0.28 |
| |
Chlor | 0.41 |
Végül az Avogadro-féle szám:
N = 68.2 · 1022.
Budapest, Szent-István reálgimnázium.
Erdős Lajos
tanár.
______________________
*) Nem mulaszthatom el, hogy e helyen ne utaljak Jean Perrin "Les atomes" c.
klasszikus munkájára, amelyben az olvasó részletes felvilágosítást talál mindazokra a kérdésekre,
amelyeket itt csak röviden érinthetek. A mű magyar fordítása a tél folyamán fog megjelenni.