Forrás: Középiskolai Mathematikai és Fizikai Lapok II.éf. 3. szám
Az atomok világában.
(Negyedik közlemény.)
A kinetikus gázelmélet, mint láttuk, megadja a molekulák valódi méreteit. Ezentúl tehát nem szabad
többé azt mondani pl. az atomsúlyok tárgyalásánál, hogy az atomok valódi nagysága nem ismeretes
és hogy az atomsúlyok puszta viszonyszámok, amelyek azt mutatják, hogy az illető atom hányszorta
nehezebb a hidrogén atomnál. Az atomsúlyok igenis viszonyszámok, azonban most már a valódi
méreteket is megadják, mert hiszen ismerjük az egységül szolgáló hidrogénatom valódi tömegét.
Midőn ezek az eredmények a mult század hetvenes éveiben ismeretessé lettek, nem fogadták őket
azzal a lelkesedéssel, amint azt várni lehetett volna. A kor nem kedvezett a kinetikus gázelméletnek
és kétkedéssel fogadtak mindent, ami vele összefüggésben volt. Kiváló gondolkodók, mint Stallo,
Mach, Ostwald versenyezve igyekeztek kimutatni, hogy az anyag molekuláris elmélete súlyos
fogyatkozásokban szenved, s legjobb esetben nem más, mint rossz munkahipotézis. Azonfölül,
mint láttuk, a meghatározás módja egynehány ellenőrizhetetlen feltevésre támaszkodik, úgy hogy az
eredmény valószínű hibája nem kevesebb, mint ± 30%, az ilyen mérések pedig a fizikában
a legeslegrosszabbak közé tartoznak.
A század vége jelentős fordulatot hozott e kérdés terén. Első sorban sikerült más, az előbbitől teljesen
eltérő módszereket találni a molekulaméretek pontos meghatározására és a módszerek, mind
kivétel nélkül azonos, vagy nagyon kevéssé eltérő eredményekre vezettek, ez pedig nem
tulajdonítható a véletlennek. Másfelől az új sugárzásokkal kapcsolatban megváltozott az anyagról
való régi felfogásunk. Az új fizika bizonyosnak látja, hogy az anyag igen is korpuszkuláris szerkezetű
és így kétszeres érdeklődéssel fordul ama módszerek felé, amelyek megadják az atom és
molekulaméreteket.
Ezek közül első sorban azt a megdöbbentően egyszerű és geniális módszert akarom ismertetni,
amely a Sorbonne nagynevű tanárától, Jean Perrin*)-től származik.
Meggondolásai oly egyszerűek és egymástól látszólag annyira távol fekvő jelenségeket kapcsolnak
egybe, hogy méltán sorozhatjuk őket az exakt tudományok klasszikus teljesítményei közé.
Mielőtt a részletekbe bocsátkoznám, az alapgondolatot akarom röviden ismertetni. Mindnyájan tudjuk,
hogy a légkör molekulái nehézségüknél fogva úgy helyezkednek el, hogy az alsó rétegekben több
van belőlük, mint a felsőkben, a levegő lent sűrűbb, fent ritkább. A ritkulás függ a magasságtól és
törvénye igen egyszerűen megállapítható. A közönséges levegőben 6 kilométerre kell emelkednünk,
hogy a sűrűség mindenkori értékének felére csökkenjen, vagyis, hogy a térfogategységben található
molekulák száma félakkora legyen, mint a kiindulásponton. Természetesen, ha a gáz sűrűbb, ez a
magasság kisebb: az oxigén atmoszférában már 5 kilométernél elérjük ezt a csökkenést, viszont az
oxigénnél 16-szorta ritkább hidrogén esetlen, ugyanezen célból 16-szorta nagyobb magasságba,
azaz 80 kilométernyire kell emelkednünk, igen, mert az oxigén molekulák 16-szorta nehezebbek, mint
a hidrogén molekulák.
Azonban az oxigén és a hidrogén molekulák nagyságát nem ismerjük. Keresnünk kell tehát egy olyan
légkört, amelynek molekulái megmérhetők. A gázak közt ilyet nem találunk, azonban közel fekszik az
a gondolat, hogy hiszen az oldatok annyi hasonlóságot mutatnak a gázakkal, hogy joggal tekinthetők
ebből a szempontból gáznak. Pontosabban szólva: vegyünk egy úgynevezett kolloid oldatot, vagy
szuszpenziót, azaz olyan oldatot, amelyben az oldott anyag részecskéi lebegnek az oldószerben
(hogy mely okból, később látni fogjuk). A kolloid aranyoldat finom szemcséi pl. nincsenek
egyenletesen eloszolva az oldószerben, hanem - mivel súlyosak, úgy, hogy a mélyebb részekben több
van belőlük, mint a magasabban. Vagyis a szuszpenzió szemcséi úgy lebegnek az oldószerben, mint
a gázmolekulák az űrben. Ha tehát a gázritkulás törvénye érvényes rájuk, meg lehet határozni azt a
magasságot, amellyel emelkedve a szemcsék száma felére csökken. A szemcsék nagyon kicsinyek
ugyan, de azért mégis direkte megszámlálhatók, sőt nagyságuk is direkte mérhető. Ha tehát a mérések
azt mutatják, hogy 1/20 mm. emelkedésnél már felére csökken a szemcsék száma, nyilvánvaló,
hogy a szemcsék annyiszor nagyobbak az oxigénmolekulánál, ahányszor az 1/20 mm. foglaltatik az
5 kilométerben, vagyis kerek számban 100 milliószor. Ily módon tehát két dolgot kell megmérnünk
1. azt a magasságot, amelynél a szemcsék száma a kiinduláspontnál érvényes szemcseszám felére
csökkent, 2. a szemcsék nagyságát. Mindkét mérés keresztülvihető és az oxigénmolekula súlya s
vele együtt az összes atomok és molekulák súlya meghatározható.
Ezt a gondolatmenetet követi Perrin. Helyszűke miatt nem térhetek ki a részletekre és csak fővonásaiban
ismertetem az eljárást, illetve a méréseknél érvényesülő elveket.
Első kérdés az, hogy ha a gázmolekulák súlyosak, mért nem sülyednek egyszerűen mindannyian az edény
fenekére? A kinetikus gázelmélet erre azt a feleletet adja, hogy ez az anyag alaptulajdonságaiból
következik. A gázmolekulák öröktől fogva mozgásban vannak és mivel tökéletesen rugalmasak, ez a
mozgás nem vész el az összeütközések alkalmával, az összes molekulák kinetikus energiája az idők
folyamán változatlan. Szóval a molekulák minden szabályosság nélkül mozognak minden irányban és
így a terjedékenység érthető: igyekeznek teljesen betölteni a rendelkezésükre álló teret.
A molekulák spontán mozgását a kolloid oldatoknál az a csodálatos jelenség helyettesíti, amelyet
először Brown angol botanikus észlelt 1827-ben. Ha valamely oldószerbe nálánál nagyobb
fajsúlyú anyagot hozunk, ez egyszerűen leül a fenékre. Nem így áll azonban a dolog, ha az illető
testecske nagyon kicsiny. Ez esetben a mikroszkopon át nézve azt látjuk, hogy ahelyett, hogy lesülyedne,
az elképzelhető legőrültebb táncot járja, felemelkedik, lesülyed, jobbra-balra mozog, de a lehető
legszabálytalanabb módon, úgy hogy bármily kis időre szorítkozunk is, sohasem mozog egyenes
vonalban, hanem még a legkisebb észlelhető idő alatt is számtalanszor változtatja mozgásirányát.
És ez a Brown-féle mozgás független minden tényezőtől, és nem veszít évtizedek alatt sem élénkségéből,
úgy látszik öröktől fogva létezik és örökké tart, mint maga a molekuláris mozgás. Wiener, Ramsay,
Delsaulx, Carbonnelle és végül Einstein adták meg a jelenség pontos magyarázatát. Az anyagról
megalkotott eredeti hipotezisre támaszkodnak: az anyag molekulákból áll és ezek a molekulák állandó
szabálytalan mozgásban vannak. Ha most a folyadékba, vagy akár a gázba egy kis test kerül, a száguldó
molekulák minden oldalról beleütköznek. Ha mármost a test nem nagyorr kicsiny, jobbról annyi
molekula ütközik bele, mint balról, felülről annyi, mint alulról (mivel a mozgások teljesen szabálytalanul
mennek végbe, érvényesül a nagy számok törvénye), a különböző irányokban nyert impulzusok
egyenlők és így algebrai összegük zéró, a test egyszerűem alámerül. Ellenben ha a test igen kicsiny,
nem érvényesül többé a nagy számok törvénye, a test hol az egyik, hol a másik oldalról kap ütést és
mivel nagyon könnyű, mindannyiszor elmozdul az ütés irányában, a molekulák pofozzák, taszigálják
és a molekuláris ütések esetlegessége magyarázza meg a Brown-féle mozgás esetlegességeit. Szóval
a kolloid oldatban lebegő részecskék valóban úgy mozognak, mint a gázmolekulák és így sűrűségük
ugyanazon törvény szerint csökken a magassággal, mint a gázoké.
Ime ez az egész módszer elméleti alapja. A legközelebbi lépés a ritkulás törvényének mathematikai
megállapítása. Képzeljünk e célból a föld színétől a magasságban egy olyan légoszlopot,
amelynek keresztmetszete = 1. Haladjunk most fölfelé h (kicsiny) magassággal. A nyomás
(p1) nyilvánvalóan kisebb lesz és pedig a h x 1 köbtartalmú gáz
súlyaival  -vel, ahol
-vel, ahol
 a sűrűséget, g
pedig a nehézség gyorsulását jelenti. Lesz tehát
a sűrűséget, g
pedig a nehézség gyorsulását jelenti. Lesz tehát
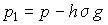
 Azonban
Azonban  kiszámítható a
Boyle-Mariotte-féle törvény alapján (a sűrűség arányos a nyomással), ha ismerjük a föld színén érvényes
légnyomást és sűrűséget
kiszámítható a
Boyle-Mariotte-féle törvény alapján (a sűrűség arányos a nyomással), ha ismerjük a föld színén érvényes
légnyomást és sűrűséget
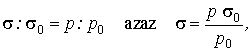
Ezek szerint
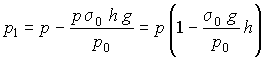
Ha most újból följebb megyünk h-val, épen így
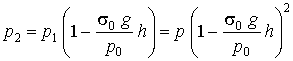
Vagyis teljes indukcióval a + nh magasságban
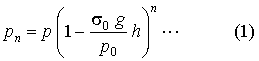
A nyomások tehát geometriai sorban csökkennek, vagyis ugyanazon h magassággal emelkedve, a nyomások
és vele együtt a sörűségek eredeti értéküknek mindig ugyanazon részével csökkennek. Így p1. ha a lépcsőn
fölfelé haladunk, a légnyomás minden lépcsőfoknál értékének 1/40.000 részével csökken. Egyúttal világos,
hogy a nyomás annál rohamosabban csökken, minél nagyobb a
 , vagyis az illető gáznak
p0 (normális) nyomás melletti sűrűsége. Sőt az (1) alatti képletből azt is kiolvashatjuk,
hogy a nyomáscsökkenés egyenesen arányos a
, vagyis az illető gáznak
p0 (normális) nyomás melletti sűrűsége. Sőt az (1) alatti képletből azt is kiolvashatjuk,
hogy a nyomáscsökkenés egyenesen arányos a  -lal, vagyis, ha pl. - mint láttuk - az oxigénben 5 km. magasságra kell emelkednünk, ha azt
akarjuk, hogy a sűrűség félakkora legyen, mint volt eredetileg, a hidrogénnél ezt csak 16 x 5 = 80 kilométer
magasságban érjük el.
Ezek után a módszer elméleti megalapozása kifogástalan és már most az a kérdés, miképen hajthatók
végre a tényleges mérések.
Budapest, Szent-István reálgimnázium.
-lal, vagyis, ha pl. - mint láttuk - az oxigénben 5 km. magasságra kell emelkednünk, ha azt
akarjuk, hogy a sűrűség félakkora legyen, mint volt eredetileg, a hidrogénnél ezt csak 16 x 5 = 80 kilométer
magasságban érjük el.
Ezek után a módszer elméleti megalapozása kifogástalan és már most az a kérdés, miképen hajthatók
végre a tényleges mérések.
Budapest, Szent-István reálgimnázium.
Erdős Lajos
tanár.
_____________________
*) Jean Perrin nevét a középiskolákban a kathódsugarakkal kapcsolatban
szokták megemlíteni. Ő mutatta ki elsőnek, hogy a kathódsugarak valóban negatív töltést hordoznak.
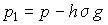
 -vel, ahol
-vel, ahol
 a sűrűséget, g
pedig a nehézség gyorsulását jelenti. Lesz tehát
a sűrűséget, g
pedig a nehézség gyorsulását jelenti. Lesz tehát
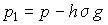
 Azonban
Azonban  kiszámítható a
Boyle-Mariotte-féle törvény alapján (a sűrűség arányos a nyomással), ha ismerjük a föld színén érvényes
légnyomást és sűrűséget
kiszámítható a
Boyle-Mariotte-féle törvény alapján (a sűrűség arányos a nyomással), ha ismerjük a föld színén érvényes
légnyomást és sűrűséget
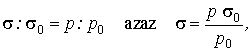
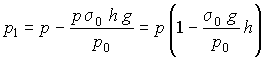
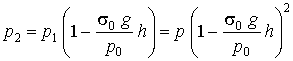
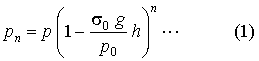
 , vagyis az illető gáznak
p0 (normális) nyomás melletti sűrűsége. Sőt az (1) alatti képletből azt is kiolvashatjuk,
hogy a nyomáscsökkenés egyenesen arányos a
, vagyis az illető gáznak
p0 (normális) nyomás melletti sűrűsége. Sőt az (1) alatti képletből azt is kiolvashatjuk,
hogy a nyomáscsökkenés egyenesen arányos a  -lal, vagyis, ha pl. - mint láttuk - az oxigénben 5 km. magasságra kell emelkednünk, ha azt
akarjuk, hogy a sűrűség félakkora legyen, mint volt eredetileg, a hidrogénnél ezt csak 16 x 5 = 80 kilométer
magasságban érjük el.
Ezek után a módszer elméleti megalapozása kifogástalan és már most az a kérdés, miképen hajthatók
végre a tényleges mérések.
Budapest, Szent-István reálgimnázium.
-lal, vagyis, ha pl. - mint láttuk - az oxigénben 5 km. magasságra kell emelkednünk, ha azt
akarjuk, hogy a sűrűség félakkora legyen, mint volt eredetileg, a hidrogénnél ezt csak 16 x 5 = 80 kilométer
magasságban érjük el.
Ezek után a módszer elméleti megalapozása kifogástalan és már most az a kérdés, miképen hajthatók
végre a tényleges mérések.
Budapest, Szent-István reálgimnázium.