Forrás: Középiskolai Mathematikai és Fizikai Lapok II.éf. 2. sz.
Az atomok világában
(Harmadik közlemény.)
Maxwell a belső súrlódás együtthatójára nézve a következő képletet vezette le
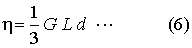
ahol G a molekulák középsebessége (ismeretes), L a szabad úthossz középértéke (ismeretlen),
d a gáz sűrűsége (ismeretes).*)
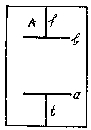 A belső súrlódás értékét azonban kísérletileg is meghatározhatjuk. Az A edényben ismert
nyomású és sűrűségű gáz foglal helyet. Ha az a korongot a t tengely körül ismert
sebességgel forgatjuk, a belső súrlódás következtében fellépő tangentialis erők lassanként mozgásba
hozzák a tőle adott távolságban felfüggesztett b korongot és azt nehány fokkal elforgatják. A
tangentialis erőkkel az f fonal torziója tart egyensúlyt. Megmérve az eltérítés szögét kiszámíthatjuk
a belső súrlódás együtthatóját. Így tehát egyenletünk közvetlenül megadja a szabad úthossz középértékét.
Oxigénnél ez a szabad úthossz 0.1 mikron, hidrogénnél körülbelül kétszerakkora (normális állapotban).
A szabad úthossz ismerete azonnal megadja az ütközések számát is. Ismerjük u. i. a molekulák sebességét
(G). Világos, hogy a molekula egyik összeütközéstől a másikig L utat tesz meg, annyiszor
ütközik össze (átlagban) 1 mp. alatt, ahányszor az L a G-ben foglaltatik. Ily módon meghatározták, hogy a normális
állapotban levő levegő molekulája másodpercenként átlagban 5000 millió összeütközést szenved el.
Ha most még emlékezetünkbe idézzük a (3) alatti összefüggést, meghatározhatjuk Q-t, vagyis
a v térfogatban foglalt molekulák felületeinek összegét. A számítást végrehajtva azt találjuk,
hogy pl. az oxigén grammolekulájára nézve (32 gramm), v = 22.400 cm3, L = 0.00001
cm a molekulák felületeinek összege nem kevesebb, mint 16 hektár. (Perrin.)
A felületek összege, mint látható, összefüggést ad a molekulák száma és a gömbalakúnak képzelt
molekulák sugara között. Még egy összefüggésre van tehát szükség, ha a kérdéses két mennyiséget meg
akarjuk határozni. Vegyünk e célból egy tetszésszerinti gázmennyiséget pl. a grammolekulát, amelyre
vonatkozólag a felületek összegét előbb meghatároztuk. Ha a gázat összenyomjuk, térfogata kisebb lesz,
a molekulák közelebb jutnak egymáshoz. Ha a nyomást fokozzuk, feltehetjük, hogy végül a gáztömeg
molekulái úgy helyezkednek el egymás mellett, mint valamely golyósor golyói. Közben a gáz
természetesen cseppfolyósodik, de ez nem okoz komplikációt. Szóval, ha a grammolekulányi gáztömeget
cseppfolyósítjuk és hideg állapotban nagy nyomásnak vetjük alá, az anyag térfogata úgy viszonylik a
molekulák valódi térfogatához, mint a golyósor által elfoglalt térfogat viszonylik a golyók valódi
térfogatainak összegéhez.
A belső súrlódás értékét azonban kísérletileg is meghatározhatjuk. Az A edényben ismert
nyomású és sűrűségű gáz foglal helyet. Ha az a korongot a t tengely körül ismert
sebességgel forgatjuk, a belső súrlódás következtében fellépő tangentialis erők lassanként mozgásba
hozzák a tőle adott távolságban felfüggesztett b korongot és azt nehány fokkal elforgatják. A
tangentialis erőkkel az f fonal torziója tart egyensúlyt. Megmérve az eltérítés szögét kiszámíthatjuk
a belső súrlódás együtthatóját. Így tehát egyenletünk közvetlenül megadja a szabad úthossz középértékét.
Oxigénnél ez a szabad úthossz 0.1 mikron, hidrogénnél körülbelül kétszerakkora (normális állapotban).
A szabad úthossz ismerete azonnal megadja az ütközések számát is. Ismerjük u. i. a molekulák sebességét
(G). Világos, hogy a molekula egyik összeütközéstől a másikig L utat tesz meg, annyiszor
ütközik össze (átlagban) 1 mp. alatt, ahányszor az L a G-ben foglaltatik. Ily módon meghatározták, hogy a normális
állapotban levő levegő molekulája másodpercenként átlagban 5000 millió összeütközést szenved el.
Ha most még emlékezetünkbe idézzük a (3) alatti összefüggést, meghatározhatjuk Q-t, vagyis
a v térfogatban foglalt molekulák felületeinek összegét. A számítást végrehajtva azt találjuk,
hogy pl. az oxigén grammolekulájára nézve (32 gramm), v = 22.400 cm3, L = 0.00001
cm a molekulák felületeinek összege nem kevesebb, mint 16 hektár. (Perrin.)
A felületek összege, mint látható, összefüggést ad a molekulák száma és a gömbalakúnak képzelt
molekulák sugara között. Még egy összefüggésre van tehát szükség, ha a kérdéses két mennyiséget meg
akarjuk határozni. Vegyünk e célból egy tetszésszerinti gázmennyiséget pl. a grammolekulát, amelyre
vonatkozólag a felületek összegét előbb meghatároztuk. Ha a gázat összenyomjuk, térfogata kisebb lesz,
a molekulák közelebb jutnak egymáshoz. Ha a nyomást fokozzuk, feltehetjük, hogy végül a gáztömeg
molekulái úgy helyezkednek el egymás mellett, mint valamely golyósor golyói. Közben a gáz
természetesen cseppfolyósodik, de ez nem okoz komplikációt. Szóval, ha a grammolekulányi gáztömeget
cseppfolyósítjuk és hideg állapotban nagy nyomásnak vetjük alá, az anyag térfogata úgy viszonylik a
molekulák valódi térfogatához, mint a golyósor által elfoglalt térfogat viszonylik a golyók valódi
térfogatainak összegéhez.  Mármost egyszerű geometriai megfontolásból kiderül, hogy a molekulák valódi
térfogatainak összege az észlelt térfogat
Mármost egyszerű geometriai megfontolásból kiderül, hogy a molekulák valódi
térfogatainak összege az észlelt térfogat 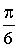 része.
T.i.
része.
T.i. 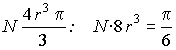 . És így új
egyenletet nyerünk a molekulák
száma és sugara között. Ha ugyanis a molekulák számát N-nel, sugarát,
mint előbb r-rel, a hideg állapotban folyósított gáztömeg észlelt
térfogatát V-vel jelöljük
. És így új
egyenletet nyerünk a molekulák
száma és sugara között. Ha ugyanis a molekulák számát N-nel, sugarát,
mint előbb r-rel, a hideg állapotban folyósított gáztömeg észlelt
térfogatát V-vel jelöljük
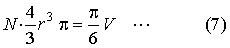
Ehhez hozzácsatolva a felületek összegére vonatkozó egyenletet
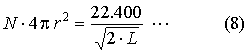
megkaptuk azt az egyenletrendszert, amelyből N és r értékeit véglegesen megállapíthatjuk.
A végzendő mérések tehát a következők:
- V a grammolekulányi gáztömeg térfogata cseppfolyósított állapotban alacsony hőmérsékleten.
- L a szabad úthossz középértéke, amelynek meghatározásához viszont a Maxwell-féle
egyenlet értelmében
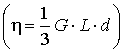 meg kell mérnünk:
meg kell mérnünk:
- ) a belső súrlódás együtthatóját,
- ) a molekulák sebességének középértékét,
- ) a gáztömeg sűrűségét.
A mérések gyakorlati kivitele nem nagyon egyszerű, azonban nem ütközik elvi nehézségekbe. Mielőtt
a mérések eredményeit közölném, még egyszer összefoglalom röviden a gondolatmenetet, hogy a
módszer minden részletében teljes világossággal álljon előttünk. A következő operációkat kellett
tehát végrehajtanunk:
- A kinetikus gázelmélet alapegyenletéből kiszámítottuk a molekulák sebességének középértékét.
- A belső súrlódás együtthatóját kísérletileg megmértük és belőle a Maxwell-féle (6) egyenlet
alapján kiszámítottuk a szabad úthossz középértékét.
- A szabad úthossz lényegesen függ a molekulák számától és méreteitől (l. a (3) és (4) alatti
egyenleteket), tehát ismerete összefüggést ad a molekulaméretek (r) és az Avogadro-féle
szám között.
- A cseppfolyósított gázat hidegállapotban lehetőleg összenyomjuk és így meghatározzuk a
molekulák térfogatainak összegét, ami szintén egy egyenletet ad r és N között.
Természetesen pontos eredményeket ez uton nem nyerhetünk, nem, mert a módszer oly feltevéseket
tartalmaz, amelyek egészen bizonyosan nem állanak, hanem csak megközelítők. Így pl. a molekulákat
gömbalakúaknak tekintettük, holott ez legföljebb az egyatomú gázakra érvényes, mint amilyen pl. az
argon, ellenben semmiesetre sem igaz a két vagy többatomú gázakra nézve. Másik ily megjegyzés
a következő. A módszer megadja a molekula sugarak nagyságát. Azonban előre világos, hogy ez
nem a valódi értéke a sugárnak. T. i. a molekulát úgy kell elképzelnünk, mint egy kis gömböt, amely
nem enged magához más molekulákat, mint a hogy a hadihajó sem enged magához ellenséges
járműveket. A molekula taszító erőket fejt ki, amely erők nem engedik közeledni a szomszédos
molekulákat. És amint a hadihajónál az ágyúk hordképessége határozza meg, hogy milyen nagy a
hatáskör, épp úgy a molekuláknál is a molekula taszító erőinek hatásgömbjét mérjük, és nem a
molekulák valódi nagyságát. A molekula sugarak itt közölt (Clausius-féle) definíciója tehát csak
első megközelítést jelent.
A hely korlátoltsága folytán nem akarom folytatni a kritikai megjegyzések felsorolását, hanem
áttérek az eredmények közlésére. Oxigénre és nitrogénre nézve
r = 1.5 · 10-8 cm, az N pedig
40 · 1022 illetve 45 · 1022.
Biztosabb eredményeket kapunk az argonnál, ahol
r = 0.1425 millimikron
és N = 62 · 1022.
A vékony hártyákkal való kísérletek tehát már nem állottak messze a molekula méretektől. A taszító
erők hatásgömbje alapján megállapított molekulasugár alig nagyobb, mint a millimikron tizedrésze. A
hidrogenatom tömege tehát kb. másfélszerese a gramm kvadrilliomodrészének, vagyis úgy viszonylik
testünk tömegéhez, valamint testünk tömege a napéhoz.
Miután a sebességeket ismerjük, könnyű meghatározni a molekulák mozgási energiájának
középértékét. 0° Celsiusnál ez nem kevesebb, mint az erg. tizbilliomodrészének a fele, vagyis
aránylag igen nagy, mert ez a munka elegendő ahhoz, hogy egy mikron átmérőjű vízcsepp egy
mikron magasságra emelkedjék.
A mérések bizonytalansága 30%.
Ezek szerint tehát a légmolekulák, amelyeket beszívunk, valamivel több, mint 1/10 millimikron
sugarú gömböcskék. 30 trillio van belőlük 1 cm3-ben (normális állapotban).
Több, mint 2 millió ilyen molekulát kellene egy fonálra feltűzni, hogy 1 millimétert kapjunk és
20 billiónak együttes súlya teszi ki a milligramm milliomodrészét. Ezek a golyócskák a puskagolyó
sebességével haladnak, azonban minden mp. alatt átlagban 5000 milliószor ütköznek össze, úgy
hogy átlagban csak 1/10 mikron utat tudnak összeütközés nélkül megtenni (Perrin).
A molekulaméreteknek és a molekulák számának közvetlen meghatározása nem lehetséges, de
mint láttuk, az emberi szellem mégis talált módot arra, hogy őket közvetett úton meghatározza. A
fizikában gyakran találunk ily közvetett mérési módokat. Ezek annál kevésbbé megbízhatók,
minél bonyolódottabbak és minél több segédhipotezist tartalmaznak. Mivel a kinetikus
gázelméletben a segédhipotezisek száma aránylag nagy, eredményeink csak akkor tekinthetők
véglegeseknek, ha még más módszerekkel is megtudjuk határozni a szóban forgó mennyiségeket
és ha az új módszerrel meghatározott eredmények megegyeznek legalább nagyjában azokkal,
amelyeket az imént közöltünk.
A következőkben látni fogjuk, hogy a megegyezés messze fölülmul minden várakozást.
Budapest, Szent-István reálgimnázium.
Erdős Lajos
tanár.
___________________________
*) Rendkívül érdekes és feltűnő, hogy a belső súrlódás (állandó hőmérséklet mellett) független a nyomástól.
Ha ugyanis a sűrűség növekszik, a gázmolekulák közelebb jutnak egymáshoz és a szabad úthossz ugyanilyen arányban kisebbedik. Ezt az első
tekintetre lehetetlennek látszó eredményt Maxwell kísérletileg is igazolta (1866). Ez a tétel a kinetikus gázelméletnek egyik legszebb alkalmazása és legnagyobb diadala.
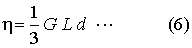
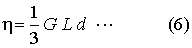
 A belső súrlódás értékét azonban kísérletileg is meghatározhatjuk. Az A edényben ismert
nyomású és sűrűségű gáz foglal helyet. Ha az a korongot a t tengely körül ismert
sebességgel forgatjuk, a belső súrlódás következtében fellépő tangentialis erők lassanként mozgásba
hozzák a tőle adott távolságban felfüggesztett b korongot és azt nehány fokkal elforgatják. A
tangentialis erőkkel az f fonal torziója tart egyensúlyt. Megmérve az eltérítés szögét kiszámíthatjuk
a belső súrlódás együtthatóját. Így tehát egyenletünk közvetlenül megadja a szabad úthossz középértékét.
Oxigénnél ez a szabad úthossz 0.1 mikron, hidrogénnél körülbelül kétszerakkora (normális állapotban).
A szabad úthossz ismerete azonnal megadja az ütközések számát is. Ismerjük u. i. a molekulák sebességét
(G). Világos, hogy a molekula egyik összeütközéstől a másikig L utat tesz meg, annyiszor
ütközik össze (átlagban) 1 mp. alatt, ahányszor az L a G-ben foglaltatik. Ily módon meghatározták, hogy a normális
állapotban levő levegő molekulája másodpercenként átlagban 5000 millió összeütközést szenved el.
Ha most még emlékezetünkbe idézzük a (3) alatti összefüggést, meghatározhatjuk Q-t, vagyis
a v térfogatban foglalt molekulák felületeinek összegét. A számítást végrehajtva azt találjuk,
hogy pl. az oxigén grammolekulájára nézve (32 gramm), v = 22.400 cm3, L = 0.00001
cm a molekulák felületeinek összege nem kevesebb, mint 16 hektár. (Perrin.)
A felületek összege, mint látható, összefüggést ad a molekulák száma és a gömbalakúnak képzelt
molekulák sugara között. Még egy összefüggésre van tehát szükség, ha a kérdéses két mennyiséget meg
akarjuk határozni. Vegyünk e célból egy tetszésszerinti gázmennyiséget pl. a grammolekulát, amelyre
vonatkozólag a felületek összegét előbb meghatároztuk. Ha a gázat összenyomjuk, térfogata kisebb lesz,
a molekulák közelebb jutnak egymáshoz. Ha a nyomást fokozzuk, feltehetjük, hogy végül a gáztömeg
molekulái úgy helyezkednek el egymás mellett, mint valamely golyósor golyói. Közben a gáz
természetesen cseppfolyósodik, de ez nem okoz komplikációt. Szóval, ha a grammolekulányi gáztömeget
cseppfolyósítjuk és hideg állapotban nagy nyomásnak vetjük alá, az anyag térfogata úgy viszonylik a
molekulák valódi térfogatához, mint a golyósor által elfoglalt térfogat viszonylik a golyók valódi
térfogatainak összegéhez.
A belső súrlódás értékét azonban kísérletileg is meghatározhatjuk. Az A edényben ismert
nyomású és sűrűségű gáz foglal helyet. Ha az a korongot a t tengely körül ismert
sebességgel forgatjuk, a belső súrlódás következtében fellépő tangentialis erők lassanként mozgásba
hozzák a tőle adott távolságban felfüggesztett b korongot és azt nehány fokkal elforgatják. A
tangentialis erőkkel az f fonal torziója tart egyensúlyt. Megmérve az eltérítés szögét kiszámíthatjuk
a belső súrlódás együtthatóját. Így tehát egyenletünk közvetlenül megadja a szabad úthossz középértékét.
Oxigénnél ez a szabad úthossz 0.1 mikron, hidrogénnél körülbelül kétszerakkora (normális állapotban).
A szabad úthossz ismerete azonnal megadja az ütközések számát is. Ismerjük u. i. a molekulák sebességét
(G). Világos, hogy a molekula egyik összeütközéstől a másikig L utat tesz meg, annyiszor
ütközik össze (átlagban) 1 mp. alatt, ahányszor az L a G-ben foglaltatik. Ily módon meghatározták, hogy a normális
állapotban levő levegő molekulája másodpercenként átlagban 5000 millió összeütközést szenved el.
Ha most még emlékezetünkbe idézzük a (3) alatti összefüggést, meghatározhatjuk Q-t, vagyis
a v térfogatban foglalt molekulák felületeinek összegét. A számítást végrehajtva azt találjuk,
hogy pl. az oxigén grammolekulájára nézve (32 gramm), v = 22.400 cm3, L = 0.00001
cm a molekulák felületeinek összege nem kevesebb, mint 16 hektár. (Perrin.)
A felületek összege, mint látható, összefüggést ad a molekulák száma és a gömbalakúnak képzelt
molekulák sugara között. Még egy összefüggésre van tehát szükség, ha a kérdéses két mennyiséget meg
akarjuk határozni. Vegyünk e célból egy tetszésszerinti gázmennyiséget pl. a grammolekulát, amelyre
vonatkozólag a felületek összegét előbb meghatároztuk. Ha a gázat összenyomjuk, térfogata kisebb lesz,
a molekulák közelebb jutnak egymáshoz. Ha a nyomást fokozzuk, feltehetjük, hogy végül a gáztömeg
molekulái úgy helyezkednek el egymás mellett, mint valamely golyósor golyói. Közben a gáz
természetesen cseppfolyósodik, de ez nem okoz komplikációt. Szóval, ha a grammolekulányi gáztömeget
cseppfolyósítjuk és hideg állapotban nagy nyomásnak vetjük alá, az anyag térfogata úgy viszonylik a
molekulák valódi térfogatához, mint a golyósor által elfoglalt térfogat viszonylik a golyók valódi
térfogatainak összegéhez.  Mármost egyszerű geometriai megfontolásból kiderül, hogy a molekulák valódi
térfogatainak összege az észlelt térfogat
Mármost egyszerű geometriai megfontolásból kiderül, hogy a molekulák valódi
térfogatainak összege az észlelt térfogat 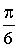 része.
T.i.
része.
T.i. 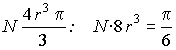 . És így új
egyenletet nyerünk a molekulák
száma és sugara között. Ha ugyanis a molekulák számát N-nel, sugarát,
mint előbb r-rel, a hideg állapotban folyósított gáztömeg észlelt
térfogatát V-vel jelöljük
. És így új
egyenletet nyerünk a molekulák
száma és sugara között. Ha ugyanis a molekulák számát N-nel, sugarát,
mint előbb r-rel, a hideg állapotban folyósított gáztömeg észlelt
térfogatát V-vel jelöljük
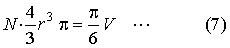
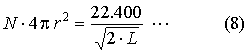
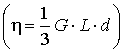 meg kell mérnünk:
meg kell mérnünk: