Forrás: Középiskolai Mathematikai és Fizikai Lapok II.éf. 1. szám
Az atomok világában.
Második közlemény.
A molekulák méreteinek és számának meghatározása a XIX. század második felének egyik
legnagyobb eredménye. A problema hosszú ideig teljesen megközelíthetetlennek látszott, míg
végre Loschmied bécsi fizikusnak sikerült hozzáférkőzni a kérdés magvához. Ő volt az
első, aki meghatározta az 1 cm3-ben foglalt gázmolekulák számát, amelyet az ő
tiszteletére ma is Loschmied-féle számnak nevezünk. Módszerének gondolatmenetét
egyszerűsített és modernizált alakjában közlöm.
E célból mindenekelőtt hivatkoznom kell a fizika és kémia néhány alapvető megállapítására. A
kérdést a gázállapotú testek tanulmányozása alapján fogjuk megoldani és így a gázak viselkedésére
vonatkozó törvényeket kell rekapitulálnom. Szükségünk van a következő törvényekre.
1. Valamely adott gáztömeg nyomása (p) és térfogata állandó hőfok mellett (v)
fordított arányban vannak, azaz pv = állandó (Boyle-Mariotte-féle törvény). A törvény,
mint tudjuk kísérleti kutatások eredménye, azonban levezethető elméletileg is. Ezt az elméleti
levezetést is tanítják a legtöbb középiskolában úgy, hogy e helyen csak a gondolatmenetét és az
eredményt akarom közölni.
Az anyag molekuláris elmélete szerint, mint minden anyag, a gázak is rendkívül nagyszámú
molekulákból állanak. Ezek a molekulák igen nagy sebességgel haladnak, teljesen betöltik a
rendelkezésükre álló teret, majd beleütköznek az edény falaiba úgy, hogy a gáz nyomása nem is
egyéb, mint ezeknek az ütközéseknek az eredménye. Azt a fizikai elméletet, amely az itt vázolt
feltevésre támaszkodik és annak következményeit foglalja magába, kinetikus gázelméletnek
nevezzük. Megalapítói Krőnig (1856) és Clausius (1857), továbbfejlesztői Maxwell és Boltzmann és
ma bátran mondhatjuk, hogy az elméleti fizikának kevés ily szép, befejezett, termékeny és
perspektívákat nyitó fejezete van.
Mármost a Boyle-Mariotte féle törvényt könnyen levezethetjük a következő módon. 1)
Vegyünk valamely adott hőmérsékleten ismert mennyiségű gáztömeget. A gáz térfogata v,
nyomása pedig p. Szorítsuk most össze a gázat úgy, hogy térfogata az eredetinek k-ad
része, v/k legyen. Világos, hogy a gáz minden köbcentiméterében most k-szor annyi
molekula lesz, mint volt előbb és így a molekulabombázás k-szor élénkebb, vagyis a nyomás
k-szor nagyobb lesz.
Ez a levezetés azonban nem elég szigorú. A kinetikus gázelmélet azonban szigorú bizonyítást is tud adni,
(Joule, Clausius stb.) amelynek eredménye a kinetikus gázelmélet alapképlete:
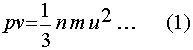
ahol p a gáz nyomása 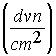 , v a gáz térfogata (cm3),
n a benne foglalt molekulák száma, m egy molekula tömege (gramm), u2
pedig a molekulák sebességeinek négyzeteiből megalkotott középérték, vagyis
, v a gáz térfogata (cm3),
n a benne foglalt molekulák száma, m egy molekula tömege (gramm), u2
pedig a molekulák sebességeinek négyzeteiből megalkotott középérték, vagyis 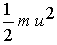 a molekulák haladó mozgásából származó kinetikus energiák középértéke. 2)
Mármost, ha meggondoljuk, hogy az adott gáztömegben n, m és u2 értékei
állandó hőmérséklet mellett nem változnak, közvetlenül láthatjuk, hogy a pv szorzat állandó. Másfelől
látnivaló, hogy a pv szorzat dimenziója munka és valóban
a molekulák haladó mozgásából származó kinetikus energiák középértéke. 2)
Mármost, ha meggondoljuk, hogy az adott gáztömegben n, m és u2 értékei
állandó hőmérséklet mellett nem változnak, közvetlenül láthatjuk, hogy a pv szorzat állandó. Másfelől
látnivaló, hogy a pv szorzat dimenziója munka és valóban
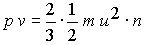
vagyis jelenti az összes molekulák kinetikus energiáinak 2/3 részét.
2. Ha a hőmérséklet változik ismeretes, hogy a Mariotte-Gay Lussae-féle törvény értelmében
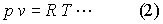
ahol T a gáz abszolut hőmérséklete (273 + t0), R pedig a gáz
kezdeti adataitól függő állandó. A molekulák mozgási energiáinak összege tehát arányos az abszolut
hőmérséklettel. Vagyis a hőmérséklet emelkedésével a molekulák sebessége folyton nő, azonban nem a
sebesség arányos a hőmérséklettel (abszolut), hanem a mozgási energia, a sebesség négyzete.
3. Az Avogadro-féle törvény. Vegyünk különböző gázakból oly mennyiségeket, hogy térfogataik
ugyanazon nyomás és ugyanazon hőfok mellett megegyezzenek. Ez esetben mindenik gáztömegben
ugyanannyi molekula foglaltatik.
A következőkben gyakran fogunk találkozni a grammolekula fogalmával. Értjük ezen azt a gáztömeget,
amelynek nagyságát grammokban az illető gáz molekula súlya adja meg. Így pl. a H molekula
súlya 2, tehát a grammolekula hidrogen éppen 2 grammot nyom, vagyis 0° hőmérséklet és 760 mm
nyomás mellett valamivel több mint 224 liter. Az Avogadro törvénye szerint közvetlenül világos, hogy
minden gáz grammolekulája ugyanekkora térfogatú. Valamely gáz grammolekulányi mennyiségében
foglalt molekulák számát az irodalomban N-nel jelöljük és Avogadro-féle számnak nevezzük.
Az itt közölt törvények legfontosabb eredménye, hogy igen egyszerűen megadják a molekulák
sebességének középértékét. Az alapképlet szerint u. i.
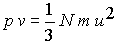
Nm nyilván nem egyéb, mint M, a gáz tömege, tehát
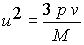
és így nyomás, térfogat és tömegméréssel azonnal meghatározhatjuk a sebesség négyzetek középértékét.
Ha különböző gázakból egyenlő térfogatokat veszünk (ugyanazon nyomás és hőmérséklet mellett, látjuk,
hogy a molekulák sebességeinek középértékei a tömegekkel, tehát a molekulasúlyokkal fordítva arányosak.
A nehéz molekulák megfelelően lassabban mozognak.
Az itt felmerült sebességekről a következő táblázat nyújt fogalmat
| | 0° | 100° | 200° |
| Oxigen | (O) | 461 m/sec | 539 m/sec | 604 m/sec |
| Hidrogen | (H) | 1843 m/sec | 2153 m/sec | 2424 m/sec |
| Szénsav | (CO2) | 392 m/sec | 458 m/sec | 515 m/sec |
Az abszolut zérus hőfokon (-273) a molekulák sebessége és vele a haladó mozgás kinetikus
energiája = 0.
Nem szabad elfelednünk, hogy itt csak középértékekről van szó, az egyes molekulák sebessége az
adottnál lehet nagyobb vagy kisebb, de a középérték adva lévén, a valószínűségszámítás módot
nyújt arra, hogy minden egyes gázra megállapítsuk a sebességek valószínű megoszlását.
Tekintetbe véve a molekulák nagy számát, belátható, hogy az egyes molekulák unos-untalan
beleütköznek társaikba. Azt a távolságot, amelyet a molekula két egymásután következő ütközés
között megtesz, szabad úthossznak nevezzük. Ez minden egyes molekulára nézve minden
időpillanatban más és más, azonban nyilvánvaló, hogy középértéke minden egyes gázra, minden
egyes hőfoknál állandó. A szabad úthossz eme középértékét a következőkben L-lel jelöljük.
Értékét először Clausius számította ki azon feltevés mellett, hogy a molekulák sebességei egyenlők.
Maxwell eltekintett ettől a megszorítástól és a következő képlethez jutott
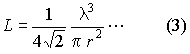
ahol 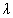 a molekulák (gömbalakú) középpontjainak
egymástól való távolsága, ill. ezen távolságok középértéke, r pedig a molekulák sugara.
Ez a törvény még más alakban is felírható. Jelöljük a térfogategységben foglalt molekulák számát
n-nel; ez esetben
a molekulák (gömbalakú) középpontjainak
egymástól való távolsága, ill. ezen távolságok középértéke, r pedig a molekulák sugara.
Ez a törvény még más alakban is felírható. Jelöljük a térfogategységben foglalt molekulák számát
n-nel; ez esetben 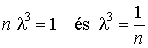 ,
vagyis
,
vagyis
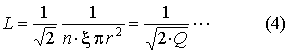
ahol Q a térfogategységben foglalt molekulák felületeinek összegét jelenti. Ez a képlet, amelynek a
következőkben nagy hasznát vesszük, nyilvánvalóan mutatja, hogy a szabad úthossz lényegesen függ a
molekulaméretektől.
Egyenletünkben több ismeretlen van, tehát belőle a szabad úthossz nem határozható meg. Hogy ezt
megtehessük új egyenletre, új megfigyelésekre, új mérésekre van szükség. Az az új jelenség, amely a
megoldáshoz vezet a gázak belső súrlódása, vagy amint a fizikában mondják, viszkozitása.
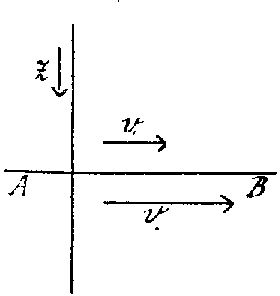 Legyen AB a válaszfelület két
gázréteg között, a felső gázréteg sebessége v1, az alsóé v2.
Már a közönséges tapasztalat is mutatja, hogy a két különböző sebesség nem maradhat meg egymás mellett,
hanem kiegyenlítődik, a gyorsabb gázréteg magával ragadja a lassúbbat és viszont veszít sebességéből. A
jelenség a kinetikus gázelmélet szerint úgy áll elő, hogy a molekulák a felső rétegből átjutnak az alsóba és
annak sebességét mérséklik, viszont az alsó rétegből átjutnak a felsőbe és fokozzák annak sebességét. Ha
most feltesszük, hogy a sebesség a z mentén haladva állandóan növekszik, könnyű belátni, hogy a
sebességek kiegyenlítődése, annál gyorsabban következik be, minél távolabbi rétegekből kerülnek át molekulák
(ezeknél u. i. a sebességkülönbség nagyobb) a másik rétegbe, továbbá minél nagyobb az így átjutó molekulák
száma. Az eredmények pontos fogalmazását a belső súrlódás együtthatójának bevezetésével érjük el.
Feltevésünk szerint a sebesség a z függvénye. A sebességkiegyenlítődést előidéző erő (P)
nyilvánvalóan arányos a sebességváltozás sebességével (sebességgradiens
Legyen AB a válaszfelület két
gázréteg között, a felső gázréteg sebessége v1, az alsóé v2.
Már a közönséges tapasztalat is mutatja, hogy a két különböző sebesség nem maradhat meg egymás mellett,
hanem kiegyenlítődik, a gyorsabb gázréteg magával ragadja a lassúbbat és viszont veszít sebességéből. A
jelenség a kinetikus gázelmélet szerint úgy áll elő, hogy a molekulák a felső rétegből átjutnak az alsóba és
annak sebességét mérséklik, viszont az alsó rétegből átjutnak a felsőbe és fokozzák annak sebességét. Ha
most feltesszük, hogy a sebesség a z mentén haladva állandóan növekszik, könnyű belátni, hogy a
sebességek kiegyenlítődése, annál gyorsabban következik be, minél távolabbi rétegekből kerülnek át molekulák
(ezeknél u. i. a sebességkülönbség nagyobb) a másik rétegbe, továbbá minél nagyobb az így átjutó molekulák
száma. Az eredmények pontos fogalmazását a belső súrlódás együtthatójának bevezetésével érjük el.
Feltevésünk szerint a sebesség a z függvénye. A sebességkiegyenlítődést előidéző erő (P)
nyilvánvalóan arányos a sebességváltozás sebességével (sebességgradiens 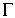 ),
a felülettel (s) és azonkívül függ a gáz anyagi minőségétől, illetőleg egy állandótól
),
a felülettel (s) és azonkívül függ a gáz anyagi minőségétől, illetőleg egy állandótól
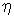 , amelynek értékét a gáz anyagi minősége
adja meg
, amelynek értékét a gáz anyagi minősége
adja meg
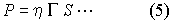
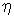 a belső súrlódás együtthatója, megadja annak
a sebességkiegyenlítő erőnek az értékét, amely fellép, ha a felület 1 cm2 és ha a sebesség
1 cm elmozdulásnál 1 m/sec-dal változik (egységnyi sebességgradiens).
(Folytatjuk).
Budapest, Szent-István rg.
a belső súrlódás együtthatója, megadja annak
a sebességkiegyenlítő erőnek az értékét, amely fellép, ha a felület 1 cm2 és ha a sebesség
1 cm elmozdulásnál 1 m/sec-dal változik (egységnyi sebességgradiens).
(Folytatjuk).
Budapest, Szent-István rg.
Erdős Lajos
tanár.
_____________________________________
1) O. D. Chwolson, Lehrbuch des Physik. 1. kötet 476.
2) Némely tankönyvben u hibásan úgy van beállítva, mint a
molekulák sebességeinek középértéke. Ez a beállítás hibás, amit azonnal
beláthatunk, ha meggondoljuk, hogy 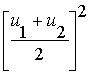 különbözik
különbözik 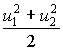 -től
ill. általánosságban
-től
ill. általánosságban 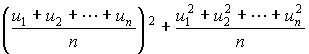 lineáris sebességek középértéke Maxwell szerint kisebb, mint négyzetes
sebességek középértéke és pedig annak
lineáris sebességek középértéke Maxwell szerint kisebb, mint négyzetes
sebességek középértéke és pedig annak 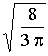 része, illetve közelítőleg 0.9 része.
része, illetve közelítőleg 0.9 része.
![]()
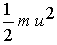 a molekulák haladó mozgásából származó kinetikus energiák középértéke. 2)
Mármost, ha meggondoljuk, hogy az adott gáztömegben n, m és u2 értékei
állandó hőmérséklet mellett nem változnak, közvetlenül láthatjuk, hogy a pv szorzat állandó. Másfelől
látnivaló, hogy a pv szorzat dimenziója munka és valóban
a molekulák haladó mozgásából származó kinetikus energiák középértéke. 2)
Mármost, ha meggondoljuk, hogy az adott gáztömegben n, m és u2 értékei
állandó hőmérséklet mellett nem változnak, közvetlenül láthatjuk, hogy a pv szorzat állandó. Másfelől
látnivaló, hogy a pv szorzat dimenziója munka és valóban
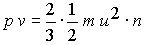
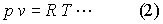
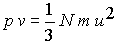
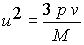
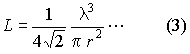
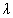 a molekulák (gömbalakú) középpontjainak
egymástól való távolsága, ill. ezen távolságok középértéke, r pedig a molekulák sugara.
Ez a törvény még más alakban is felírható. Jelöljük a térfogategységben foglalt molekulák számát
n-nel; ez esetben
a molekulák (gömbalakú) középpontjainak
egymástól való távolsága, ill. ezen távolságok középértéke, r pedig a molekulák sugara.
Ez a törvény még más alakban is felírható. Jelöljük a térfogategységben foglalt molekulák számát
n-nel; ez esetben 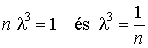 ,
vagyis
,
vagyis
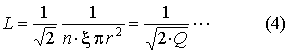
 Legyen AB a válaszfelület két
gázréteg között, a felső gázréteg sebessége v1, az alsóé v2.
Már a közönséges tapasztalat is mutatja, hogy a két különböző sebesség nem maradhat meg egymás mellett,
hanem kiegyenlítődik, a gyorsabb gázréteg magával ragadja a lassúbbat és viszont veszít sebességéből. A
jelenség a kinetikus gázelmélet szerint úgy áll elő, hogy a molekulák a felső rétegből átjutnak az alsóba és
annak sebességét mérséklik, viszont az alsó rétegből átjutnak a felsőbe és fokozzák annak sebességét. Ha
most feltesszük, hogy a sebesség a z mentén haladva állandóan növekszik, könnyű belátni, hogy a
sebességek kiegyenlítődése, annál gyorsabban következik be, minél távolabbi rétegekből kerülnek át molekulák
(ezeknél u. i. a sebességkülönbség nagyobb) a másik rétegbe, továbbá minél nagyobb az így átjutó molekulák
száma. Az eredmények pontos fogalmazását a belső súrlódás együtthatójának bevezetésével érjük el.
Feltevésünk szerint a sebesség a z függvénye. A sebességkiegyenlítődést előidéző erő (P)
nyilvánvalóan arányos a sebességváltozás sebességével (sebességgradiens
Legyen AB a válaszfelület két
gázréteg között, a felső gázréteg sebessége v1, az alsóé v2.
Már a közönséges tapasztalat is mutatja, hogy a két különböző sebesség nem maradhat meg egymás mellett,
hanem kiegyenlítődik, a gyorsabb gázréteg magával ragadja a lassúbbat és viszont veszít sebességéből. A
jelenség a kinetikus gázelmélet szerint úgy áll elő, hogy a molekulák a felső rétegből átjutnak az alsóba és
annak sebességét mérséklik, viszont az alsó rétegből átjutnak a felsőbe és fokozzák annak sebességét. Ha
most feltesszük, hogy a sebesség a z mentén haladva állandóan növekszik, könnyű belátni, hogy a
sebességek kiegyenlítődése, annál gyorsabban következik be, minél távolabbi rétegekből kerülnek át molekulák
(ezeknél u. i. a sebességkülönbség nagyobb) a másik rétegbe, továbbá minél nagyobb az így átjutó molekulák
száma. Az eredmények pontos fogalmazását a belső súrlódás együtthatójának bevezetésével érjük el.
Feltevésünk szerint a sebesség a z függvénye. A sebességkiegyenlítődést előidéző erő (P)
nyilvánvalóan arányos a sebességváltozás sebességével (sebességgradiens 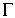 ),
a felülettel (s) és azonkívül függ a gáz anyagi minőségétől, illetőleg egy állandótól
),
a felülettel (s) és azonkívül függ a gáz anyagi minőségétől, illetőleg egy állandótól
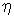 , amelynek értékét a gáz anyagi minősége
adja meg
, amelynek értékét a gáz anyagi minősége
adja meg
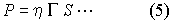
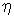 a belső súrlódás együtthatója, megadja annak
a sebességkiegyenlítő erőnek az értékét, amely fellép, ha a felület 1 cm2 és ha a sebesség
1 cm elmozdulásnál 1 m/sec-dal változik (egységnyi sebességgradiens).
a belső súrlódás együtthatója, megadja annak
a sebességkiegyenlítő erőnek az értékét, amely fellép, ha a felület 1 cm2 és ha a sebesség
1 cm elmozdulásnál 1 m/sec-dal változik (egységnyi sebességgradiens).
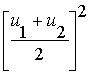 különbözik
különbözik 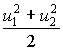 -től
ill. általánosságban
-től
ill. általánosságban 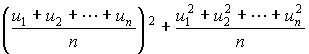 lineáris sebességek középértéke Maxwell szerint kisebb, mint négyzetes
sebességek középértéke és pedig annak
lineáris sebességek középértéke Maxwell szerint kisebb, mint négyzetes
sebességek középértéke és pedig annak 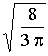 része, illetve közelítőleg 0.9 része.
része, illetve közelítőleg 0.9 része.