RADNAI GYULA

Elektromosságtani alapfogalmaink
kialakulása

Első rész

Kvalitatív elektrosztatika

Első pillantásra meglepő, mégis magával ragadó a fizika fejlődésének évszázadonkénti korszakolása, ahogyan ez ebben az előadás-sorozatban történik.1

Már a következő rápillantásra látszik azonban, hogy ez a felosztás is – mint minden ilyen nagyvonalú rendezés – meglehetősen erőltetett. A XVIII. századi fizikából az elektromosságtan fejlődését kiragadni csak erőszakoltan lehet. Ebben a században élt és alkotott például Euler, ekkor alakult ki a newtoni fizika differenciálegyenletekre épülő alkalmazása a mechanikában. Ugyancsak ekkor élt Lavoisier, aki megcáfolta a flogisztonelméletet, de maradéktalanul hitt a hő fluidumelméletében, aminek alapján Fourier kidolgozta a hővezetés elméletét. Másrészt az elektromosságtan kifejlődésének igazi százada a következő, a XIX. század, amikor Volta, Ampère, Faraday, Maxwell, Hertz munkássága nyomán olyan csúcsokra ért fel az elektromosság tudománya, hogy alkalmazásaival teljesen átalakította az ember környezetét, életét, kultúráját. Természetesen a hőtan is a XIX. században ért igazán termodinamikává. Mind a hőtannak, mind az elektromosságtannak a XVIII. század volt a gyerekkora, és mindkét tudomány a XIX. században vált felnőtté.

Most, ebben az előadásban azonban csak az elektromosságtan alapfogalmainak kialakulását követjük végig, ami nagyrészt a XVIII. századra esett.

Elsősorban az elektromos töltés, feszültség, kapacitás fogalmairól van szó. A mai diák számára ezek a szavak közismertek, és eszébe se jut, hogy ezeket is ki kellett találnia, be kellett vezetnie valakinek a tudományba. Pedig így van: az elektromosságtan története főképp azért tanulságos, mert példáján keresztül bepillantást nyerhetünk a fizika és általában a természettudomány fejlődésébe. Arra a buktatókkal teli, zegzugos útra, mely a jelenségek észrevételén, felfedezésén, tanulmányozásán át az alapfogalmak bevezetéséhez s a velük megfogalmazható, rájuk érvényes elméletek kialakulásához vezet.
1. ábra. "Az elektroszkóp vagy
villamosságmutató"
Tekintsük az 1. ábrát! Ez az ábra egy csaknem száz évvel ezelőtti könyvből való, de bármelyik mai fizika tankönyvben szerepelhetne. Sőt szerepelhetett volna már kétszáz évvel ezelőtt is, hiszen amit mutat, az az elektromosság egyik, akkor már ismert alapjelensége. Az aláírás szerint: Az elektroszkóp, vagy villamosságmutató. Villamos test közeledését megérzi.

A jelenség annyira fontos, hogy kísérlettel is bemutatjuk. Kell hozzá egy megdörzsölt műanyagrúd és egy elektroszkóp. Ha a megdörzsölt rudat felülről az elektroszkóphoz közelítjük, az elektroszkóp lemeze(i) kitér(nek). Még hozzá se ért a rúd az elektroszkóphoz, de az már jelez! Hogyan értelmezhetjük ezt a jelenséget? Például úgy, hogy a rudat valami elektromos atmoszféra veszi körül, amit megérez az elektroszkóp. Bizonyára vannak, akik a rúd aurájáról beszélnének; ez a kifejezés se lenne jobb, se rosszabb a rúd atmoszférájánál. Mondhatjuk persze, hogy ez az elképzelés a Faraday-féle erőtérfogalom előképe, de legyünk óvatosak az értelmezéssel. Az biztos, hogy ezzel a kísérlettel felfedeztünk valamit, ami további tanulmányozásra érdemes.

Az iskolában, ahol okosan tanítják a fizikát, gyakran él a tanár ilyen “felfedeztető” kísérletekkel. Ezzel mintegy a tudomány által is követett útra kívánja terelni a tanulót, és ez nagyon helyes. Csak az a bökkenő, hogy az elektromosság alapjelenségeinek felfedezéséhez a történelem során még nem állt rendelkezésre elektroszkóp! Az elektroszkópot ki kellett találni, mint ahogy azt is ki kellett kísérletezni, hogy mivel dörzsölve tudunk egy tárgyat elektromossá tenni. Galileinek se adott kezébe senki se lejtőt, hogy azzal kísérletezzen! A természettudományos felfedezés lényege, hogy ki kell találni mindazokat az eszközöket is, melyekkel a jelenség érdemben megvizsgálható. Fogunk erre még példát látni.

Mielőtt azonban a XVIII. századi tudomány részleteibe bocsátkoznánk, meg kell emlékeznünk az elődökről. Egy XVI. és egy XVII. századi tudós munkásságát fogjuk röviden áttekinteni. Mindketten szerepelnek A fizika fejlődése c. posztersorozat első tábláján, amelyet e tanulmány szerzője által a 70-es évek második felében tervezett. Itt 1450-től 1980-ig születési sorrendben, egymás fölött láthatók a legismertebb fizikusok életsávjai. (Ugyancsak jól látszik ezen a poszteren a tudomány fejlődésének “exponenciális” jellege, mely egyesek szerint mostanában lelassult és inflexiós pontjához közeledik.) Simonyi Károly A fizika kultúrtörténete c. könyvének ideillő táblázatában 1600-tól 1900-ig van feltüntetve az elektromágneses jelenségek felfedezésének kronológiája. Itt is szerepel mindkét tudós.


William Gilbert		        
Otto von Guericke		        
Pieter van Musschenbroek

A legelső, akinek neve joggal került be az elektromosság és a mágnesség történetébe: William Gilbert (1544-1603). Shakespeare korában élt, a XVI. századi Angliában. I. Erzsébet királynő (VIII. Henrik és Boleyn Anna lánya) élete vége felé házi orvosául is fogadta a Camridge-ben végzett, nagy tekintélyű tudós orvosprofesszort, aki végül már egész Londonra és környezetére érvényes felügyeleti hatáskörrel rendelkezett.

Gilbert igazi természettudós volt. De magnete magneticisque corporibus et de magno magnete Tellure (A mágnesről, a mágneses testekről és a Föld mágnességéről) című műve, mely 1600-ban jelent meg (természetesen latinul), a mágnességhez fűződő, korabeli misztikus elképzeléseket volt hivatva megcáfolni. Ebben a művében magyarázta meg Gilbert a hajózásban nélkülözhetetlen mágneses iránytű működését, felállítva azt a hipotézist, hogy maga a Föld is egy óriási mágnes. Az iránytű északi pólusa mutat a földrajzi Északi-sarok felé, ott van tehát a Föld mágneses déli pólusa.. A kételkedők meggyőzésére állítólag készített is vasból egy földgömbmodellt, melyet felmágnesezett és illusztrációként körbe-körbe vezetett rajta egy piciny iránytűt.

Vizsgálta a megdörzsölt borostyánkő hatását is. Megállapította, hogy ez egészen más jellegű, mint a mágnesség. A mágnességet inkább a gravitációhoz hasonlította, mindkettőben valami megszüntethetetlen “őserőt” látott. Úgy tapasztalta, hogy többféle test is mutathat dörzsölésre “borostyánkőhatást”. Ő vette elő erre a hatásra az elektricitás szót is, amelyet Arisztotelész szerint Thalesz használt először, minthogy a borostyánkövet az ógörög nyelvben elektronnak mondták.

Gilbert fontosnak tartotta azt a tapasztalatát, hogy a dörzsölésre fellépő hatás könnyen megszüntethető. Ha például benedvesítjük a megdörzsölt rudat, a hatás elmúlik, és utána se lehet a vizes rudat dörzsöléssel az előbbi állapotba hozni. Bezzeg a mágnességre nincs hatással a nedvesség! Vagyis Gilbert számára a mágnesség alapvető, az elektromosság pedig csupán mesterségesen előidézhető tulajdonsága lehetett bizonyos testeknek.

Ma is úgy gondoljuk, hogy a sztatikus mágnességnek semmi köze a sztatikus elektromossághoz, de hogy mennyire vigyázni kell a jelenségekből levont következtetésekkel, vizsgáljuk meg, hat-e a megdörzsölt műanyagrúd a mágneses iránytűre! Jól látható, hogy hat rá.

Mégsem volt igaza Gilbertnek? Meg a mai tudománynak?

Dehogynem. Azt kell csak észrevenni, hogy minden iránytű vasból van, a vas pedig fém, és benne is keletkezik elektromos megosztás, ha a megdörzsölt műanyagrúd közelébe kerül. A rúd elektromos terében az iránytűből keletkezett elektromos dipólusra forgatónyomaték hat, ami elfordítja az iránytűt. Nyilván akkor is elfordítaná, ha ez a fémtű nem lenne mágneses. (Igaz, és éppen az Einstein-évben kiváltképp fontos megemlítenünk, hogy az elektromágneses hullámban a változó elektromos és mágneses terek szorosan összekapcsolódnak egymással, s a speciális relativitás elmélete meggyőző átjárást teremt az elektromos és a mágneses terek között, de itt még csak sztatikus terekről van szó, amelyek alapvetően különböznek egymástól.)

Gilbert feltámasztotta kétezer éves tetszhalott állapotából az elektricitás szót, s ezzel nevet adott egy új tudománynak, az elektromosság tudományának.

Gilbert halála előtt egy évvel megszületett a kontinensen az a fizikus, aki az első elektromosságfejlesztő gépet feltalálta: Otto von Guericke (1602-1686). Magdeburgban született, gazdag patrícius család gyermekeként. 15 éves volt, amikor a lipcsei egyetemre felvették; 16, amikor menekülnie kellett innen a kitört harmincéves háború miatt; 18, amikor apja váratlanul meghalt, ő pedig Jenában kezdte újra az egyetemet, amit azután Leydenben fejezett be. Építészetet, mechanikát, matematikát, geometriát hallgatott, de nem szerzett semmiféle fokozatot. Elutazott Franciaországba, majd Angliába, végül visszatért szülővárosába, ahol városi tanácsosként az építési ügyekért volt felelős. Ebben a minőségében volt kénytelen végignézni, ahogy 1631-ben Tilly katonái lerombolták és felégették a várost. Utána vezető szerepet játszott az újjáépítésben.

A szerencsétlen harmincéves háború 1648-as befejezése előtt két évvel őt választották Magdeburg polgármesterévé, és az maradt harminc éven át, egészen 1676-ig. Közben a város ügyeinek intézése mellett maradt ideje fizikai kísérletezésre, sőt találmányainak “menedzselésére” is. Invenciózus, ötletgazdag feltaláló volt. Kopernikusz híveként megpróbálta az “űrt” a földön is előállítani, így találta fel a légszivattyút. Torricelli kísérletét időjárásjelző barométerré fejlesztette. Jól ismert a “magdeburgi félgömbökkel” tartott látványos bemutatója, mellyel 1654-ben Regensburgban, 1657-ben Bécsben, 1661-ben Berlinben vívta ki császári és királyi udvarok elismerését.

Témánk szempontjából legfontosabb találmánya 1663-ban született meg. Nem tudni, miért kezdett bele hatvanévesen egy teljesen új jelenségkör kutatásába. Azt se, hogy miért pont a ként választotta kutatása tárgyául, csak az biztos: rájött, hogy a felolvasztott, majd megszilárdult ként megfelelően dörzsölve elektromossá lehet tenni, még pedig jobban, mint bármi mást.

A kéngolyón tengelyt szúrt át, a tengelyt rögzítette egy faállványon és hajtókart szerelt rá. Miközben egyik kezével a hajtókart forgatta, másik kezét a forgó kéngolyóhoz nyomta, s a golyó a dörzsölés hatására elektromossá vált. Ki is lehetett venni a kéngolyót az állványból és az elektromossággal tovább lehetett kísérletezni. Mindez jól látható az 1672-ben Amszterdamban kiadott könyve egyik ábráján (2. ábra)

2. ábra. Guericke kísérlete
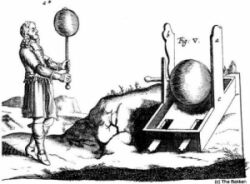Guericke nem elégedett meg ennyivel, kísérletezett tovább. A kéngolyót üveggömbbe helyezte, azt dörzsölte. Dörzsöléshez már nemcsak a tenyerét használta, hanem különböző anyagú párnákat nyomott neki a forgó golyónak. Az üveggömbből kiszivattyúzta a levegőt, ekkor dörzsölés közben észrevett bizonyos felvillanásokat az üveggömbben – így ő fedezte fel és tanulmányozta először az alacsony nyomáson létrejövő elektromos kisüléseket.

Guericke volt a XVII. század egyik jelentős kísérleti fizikusa. Magányos kísérletező, aki egyetemen nem adott elő s így tanítványa se volt. Elektromozó gépe azonban elterjedt egész Európában; a főúri szalonokban épp olyan szívesen kísérleteztek vele, mint az egyetemeken.

Tökéletesítették a gépet: javították a meghajtást, az üveggömböt lapos üvegkorongra cserélték, amelyhez foncsorozott párnát nyomtak, hogy még több elektromosságot nyerjenek vele. Sok-sok tapasztalat gyűlt már össze, miközben a kísérletezőknek fogalmuk se volt arról, hogy valójában mi az az elektromosság, amit előállítottak. Nem tudták mérni, mert nem volt hozzá műszerük, nem tudták tárolni, mert elképzelésük se volt arról, milyen edényben lehetne az elektromosságot összegyűjteni.

Ezt azért megpróbálták.

Az elektromosság tudományát ekkor egy újabb véletlen felfedezés segítette tovább a fejlődés zegzugos útján, még pedig Leidenben, Hollandiában. Ez azonban már a XVIII. században történt. Pieter (Petrus) van Musschenbroek (ejtsd: müsz-sön-bruk; (1692-1761), a híres holland professzor akkor már hatodik éve tanított a leideni egyetemen. Előtte Duisburgban, majd Utrechtben tanított “fizikát” (előtte csak természetfilozófiának nevezték ezt a tárgyat arrafelé). Szülővárosa volt Leiden, az egyetemet is itt végezte el. Itt szerzett fokozatot először orvostudományból, azután doktorált természetfilozófiából. Már gyerekkorában megismerkedett különféle tudományos eszközökkel, műszerekkel a család műhelyében, ahol légszivattyút, mikroszkópot és távcsöveket is készítettek. Az egyetem elvégzése után pedig Londonba látogatott, ahol Newtonnal is megismerkedett, és feltétlen híve lett a newtoni fizikának. Musschenbroek Elementa physicae c. egyetemi tankönyve több kiadásban is megjelent, még Magyarországra is eljutott a külföldön tanuló magyar diákok jóvoltából.

1745 novemberében kezdett azokba az elektromos kísérletekbe, melyek során a dörzsöléssel keltett elektromosság megőrzésére, tárolására keresett valamilyen eszközt és módszert. Fémrúdon már el tudta vezetni az elektromosságot bárhová, de azt szerette volna elérni, hogy az elektromosság valahogy bele is folyjon egy edénybe, ahol hosszabb ideig eltartható. Tudta, hogy a víz vezeti az elektromosságot, talán egy üveg víz alkalmas lehet az elektromosság tárolására (3. ábra). Nem egyedül kísérletezett a professzor, mindig volt, aki segített neki. A segítség, aki egyik kezében tartotta a háromnegyedéig vízzel telt palackot, másik kezével véletlenül hozzáért ahhoz a fémrúdhoz, amiből az elektromosság áramlott egy ideje a vízbe. Ez volt az a pillanat, amikor a segítség még felkiáltani se bírt a kapott áramütéstől. A professzor pedig – igazi kísérleti fizikushoz illő módon – saját maga is kipróbálta utána a kísérletet. Azután ő se bírt megszólalni.

3. ábra. A Musschenbroek-kísérlet a leideni palackkal
1746 januárjában levélben számolt be a borzasztó élményről tudóstársának, Réaumurnek, és csakhamar elterjedt az eset híre. Az egész felfedezés valahogy “benne volt a levegőben”, Musschenbroektól függetlenül egy észak-német amatőr kísérletező, bizonyos Kleist (1700-1748) kanonok is feltalálta ugyanezt a nagy kapacitású kondenzátort, ami végül is Nollet (1700-1770) francia fizikus nyomán "leideni palack" néven terjedt el a világban.

Nagyon sokan végeztek elektromos kísérleteket akkoriban, s a kísérletek híre még Amerikába is eljutott. Ez lett az elektromosságtan szerencséje, mert egy nagyszerű, találékony kísérletező, mellesleg kiváló politikus és államférfi, meggyőző kommunikációs és menedzseri készségekkel megáldott szakember, Benjamin Franklin (1705-1790) szintén hasonló kísérletekbe kezdett Philadelphiában. A mai 100 dolláros bankjegyen az ő arcképe látható, igaz, már öregkorából. Ha pedig egy államban valaki akkora tiszteletnek örvend, hogy legfontosabb bankjegyükön őrzik meg arcvonásait, annak komoly oka van. Valóban, a Bostonban született szegény gyerekre születésekor még ugyanaz a sors várt, mint tizenöt testvérére. Ő mégis többre vitte, mint bármelyikük, s ezt nemcsak már említett sokféle tehetségének, hanem rendkívül céltudatos és fegyelmezett életvitelének köszönhette. Naplót vezetett, melyből később könyvet is írt a mindenkori ifjúság okulására. Magyarországon többek között Széchenyi Istvánra volt nagy hatással.


Benjamin Franklin		        
Giovanni Battista Beccaria		        
Henry Cavendish

1752-ben, 47 éves korában kezdett foglalkozni az elektromossággal. Akkor már gazdag ember volt, nyomdatulajdonos és hírlapkiadó. Addig is folytonosan képezte magát, nyelveket tanult, nemcsak a modern nyelveket, hanem a klasszikus latint és görögöt is. A közéletben aktívan részt vett: nemzetőrséget szervezett, tűzoltó egyesületet alapított, akadémiát, könyvtárat létesített. Pennsylvania kormányzója őt küldte tárgyalni Európába. Olyan sikeresen tárgyalt, hogy nemsokára őt választották meg kormányzónak. Nagy szerepe lett később az amerikai Függetlenségi Nyilatkozat megszületésében, az Amerikai Egyesült Államok létrejöttében.

Európában akkor az elektromosság “kétfolyadékos” elmélete dívott, melyet a fiatalon elhunyt francia Dufay (1698-1739) fogalmazott meg legtisztábban. Eszerint kétféle elektromosság létezik, az “üvegelektromosság” és a “gyantaelektromosság”. Az egyneműek taszítják, a külön neműek pedig vonzzák egymást.

Franklin rendező szelleme azonnal változtatott ezen a felfogáson. Azt mondta, hogy elég egyfajta elektromosságot feltételezni, melynek feleslege, vagy éppen hiánya magyarázza a testek speciális elektromos viselkedését. El is nevezte az üvegelektromosságot pozitív elektromosságnak, a gyantaelektromosságot pedig – az üvegelektromosság hiányának tekintve – negatív elektromosságnak. (Hogy miért épp az üvegelektromosságot választotta pozitívnak, azt ma már senki se tudja megmondani.) Azután elnevezte “töltésnek” (charge) a felvitt elektromosságot – Franklin jól sikerült kifejezése a mai napig él a tudományban!

Kereste és meg is találta az ember által létrehozott elektromos kisülések gigantikus megfelelőjét a természetben, mégpedig a villámlásban. (Már James Watt is sejtett valamit, sétabotjának borostyánkő gombja saját kezének dörzsölésétől könnyen feltöltődött, időnként szikrázott is, mintha csak villámlana – de túlságosan betöltötte Watt gondolatait a gőzgép tökéletesítése, és nem mélyedt el hipotézisének vizsgálatában úgy, mint Franklin.) Az égi és a földi, laboratóriumi villámlás egyformán elektromos volta persze hipotézis volt mindaddig, amíg kísérletekkel nem sikerült alátámasztani.

Franklin kísérlete meglehetősen egyszerű volt: vihar előtti barátságtalan időben kiment a mezőre és felengedett egy sárkányt (4. ábra). Olyat, amivel a gyerekek és játékos kedvű felnőttek szórakoznak napsütötte, szép időben. Fémdarabokat erősített a sárkányra, hogy azok a felhőbe érve feltöltődhessenek elektromossággal. Az esőre álló időben, a páratelt levegőben azonban a zsinór átnedvesedett, ezáltal jó vezetővé vált. Franklin szerencsére még jókor engedte el és kötötte ki egy karóhoz a sárkány nedves zsinórjának végét, így megfigyelhette, ahogy a zsinórvégről szikrák ugrálnak át a földbe.

4. ábra. Franklin kísérlete a sárkánnyal egy 1877-beli képen

Így született meg Franklin praktikus agyában a villámhárító ötlete!

Hihetetlenül gyorsan terjedt el Franklin találmánya – talán csak Röntgen felfedezése futott be ehhez hasonló gyors karriert a XIX. század végén. Franklint már a következő évben, 1753-ban tagjául választotta és Copley-éremmel tüntette ki a londoni Royal Society. Csak a hiú angol királynak nem tetszett Franklin megoldása, és ahol csak hatalma engedte, fémgömbre cseréltette ki a villámhárító hegyes fémcsúcsát.

Ma is vannak, akik azt hiszik, hogy a villámhárítónak az a funkciója, hogy a villám belecsapjon. Hogy oda csapjon a villám és ne máshova. Pedig Franklin az elektromos csúcshatást állította találmánya szolgálatába, azt a hatást, amellyel egy csúcs meg tudja akadályozni, hogy az őt hordozó test túlságosan feltöltődjön.

A villámhárítónak az a feladata, amit a neve is kifejez, hogy elhárítsa, megakadályozza a villám létrejöttét!

Idézzünk fel csak egy kísérletet! Tudjuk, hogy a megdörzsölt műanyagrúd közelítésekor jelez az elektroszkóp. Ha ezután eltávolítjuk a feltöltött rudat, az elektroszkóp is visszaáll alaphelyzetébe. Ha fémcsúcsot teszünk az elektroszkóp érzékelőtányérjára, és ezután közelítjük a feltöltött rudat a fémcsúcs felé, az elektroszkóp már sokkal messzebbről jelez, mint az előbb. Ha eltávolítjuk a rudat, az elektroszkóp továbbra is jelez, tehát feltöltődött!

A csúcs az oka mindennek: szemléletesen szólva töltést szívott le a megdörzsölt műanyagrúdról. Ugyanígy tud a villámhárító fémcsúcsa töltést leszívni a közelítő viharfelhőből, ezáltal csökkenti a föld és a felhő közötti feszültséget, ami villámlást tudna kiváltani. A villámhárító közvetítésével állandó áram folyik a föld és a felhő között, de ez nem veszélyes a közelében lévő emberekre, állatokra. (Persze, ha átmenne rajtuk, azt azért megéreznék.) Sokkal kisebb ez az áram annál, mint ami egyetlen villám esetén lép fel, és nem kíséri olyan látványos fény- és hangjelenség sem, mint a valódi villámot.

Éles eszével és praktikus gondolkodásával Franklin egy sor olyan jelenséget tudott leegyszerűsíteni és érthetővé tenni, amit a tudósok általában túl bonyolultnak tartottak. Jellegzetes példája ennek az ún. “Franklin-tábla”, ami egy mindkét oldalán fémfóliával (részben) bevont üveglemez. A két fémfólia pontosan ugyanakkora és egymással szemben helyezkedik el. Franklin ezzel kitalálta a legegyszerűbb kondenzátort, a síkkondenzátort. Akkor, amikor Európában még csak a leideni palacknál tartottak.

Nevezetes kísérleteit is többen megpróbálták megismételni, sőt továbbfejleszteni. Oroszországban Nagy Péter, a tudományt is pártfogoló cár, tudósokat hívott mindenhonnan az általa alapított új városba, Szentpétervárra. Sok neves svájci matematikust nyert meg, közülük is a leghíresebb, Leonhard Euler (1707-1783) még Nagy Péter halála után is évtizedeken át ott dolgozott.

Egy német származású tehetséges tudós, bizonyos Georg Wilhelm Richmann, aki egyidős volt Lomonoszovval és ugyancsak komoly eredményei voltak már a hőtanban, elektromos kutatásokat végzett. Kísérleteihez megpróbálta elektromos töltésforrásként használni Franklin sárkányát. Saját szentpétervári házából engedte fel a sárkányt, s még ügyelt is arra, hogy a zsinór alsó végét jól elszigetelje a földtől. 1753. július 26-án, miközben azt figyelte, jön-e már az égből az elektromosság, minden bizonnyal túl közel hajolt a zsinór végéhez, s egy pillanat alatt a tudomány hősi halottjává vált.

Franklin Benjamin – itthon csak így emlegették – nagy tiszteletnek örvendett Magyarországon. Önéletírását, amely Széchenyire oly nagy hatással volt, magyarra is lefordították. A Franklin Társulat lett az egyik legnagyobb hazai könyv- és hírlapkiadó vállalat a XIX. század végére. Itt adták ki a Vasárnapi Újságot és a Budapesti Szemlét. Nem sokan tudják, ezért érdemes megemlíteni, hogy a “Franklin Irodalmi és Nyomdai Részvénytársulat” 1873-ban vette fel Franklin nevét, mellesleg elődje volt az a “Landerer és Heckenast” nyomda, ahol a Nemzeti dalt és a 12 pontot kinyomtatták 1848-ban.

 

Fluidumelméletek

A XVIII. században párhuzamosan fejlődött a fizika akkori két legfontosabb ága, az elméleti mechanika és a kísérleti anyagtudomány.

Az elméleti mechanikát Newton követői, főleg matematikai vénával megáldott tudósok fejlesztették magas szintre. Tudósok, akik értették a differenciál- és integrálszámítást, akik képesek voltak a mechanikai problémák kezelésére differenciálegyenleteket felállítani és megoldani. Egyszerre művelték és kutatták a matematikai analízist és az elméleti mechanikát. Nem is véletlen, hogy később, a XIX. században még azokat a tudósokat is matematikusnak hívták, akiket a XX. században már elméleti fizikusnak neveztek. Nagyszerű eredmények születtek a XVIII. századi elméleti mechanikában, s a korabeli tudósok meggyőződésévé vált, hogy akkor tekinthető egy fizikai tapasztalati törvény igazán tudományosnak, ha a mechanika törvényeire visszavezethető, azokból levezethető.

A kísérleti anyagtudomány viszont a jelenségek mind szélesebb körét tárta fel és vetette beható vizsgálat alá. Még nem is olyan régen volt, hogy az alkímia művelői titkos receptek után kutattak, melyek segítségével olcsó fémekből, például ólomból vagy higanyból lehet majd aranyat előállítani. Császárok és királyok voltak e kutatások pártfogói. Ma már turistalátványosság a prágai Hradzsinban az az “Arany utcácska”, ahol a várfalba vájt piciny műhelyekben működtek Rudolf császár aranycsinálói.

A XVIII. századra ugyan nem sikerült aranyat előállítani, de annyi tapasztalat, a jelenségek olyan változatossága tört utat magának, hogy szükség volt valamilyen elméleti rendteremtésre. Abban a században, amikor a Nagy Francia Enciklopédia megszületett, nem maradhattak rendező elvek nélkül a kísérleti anyagtudományok sem. Így születtek meg az ún. fluidumelméletek.

A fluidum a fizikában valamilyen áramlásra képes anyagot jelöl, ez gáz is, folyadék is lehet, a latin kifejezés eredeti jelentése azonban folyadék. Legegyszerűbb lesz, ha a víz példáján világítjuk meg a fluidumra vonatkozó alapvető fogalmakat és összefüggéseket.

Egy tartályban lévő víz esetén két adat látszik fontosnak: a víz mennyisége és szintje a tartályban. Nagyon fontos tudnunk ezenkívül azt is, hogy megadott mennyiségű vizet hozzátöltve a tartályban lévő vízhez, mennyivel nő ott a víz szintje. A tartályba öntött víz mennyiségének és a hatására létrejövő vízszintemelkedésnek az arányát nevezhetjük a tartály aktuális kapacitásának. (Vigyázat: ez a kapacitás nem a tartály térfogatától függ, hanem a mostani példában inkább a víz felszínével arányos mennyiség. Nagyobb vízfelszín esetén több vizet kell még betölteni, hogy ugyanannyival nőjön a vízszint.)

Képletesen a következőket írhatjuk:

M = C∙(H2-H1),
vagy még egyszerűbben
M = C ∙∆H.

(M a betöltött víz mennyisége, ∆H = H2-H1a vízszint emelkedése, C a tartály kapacitása.) Bonyolult alakú tartály esetén a most definiált kapacitás a mindenkori vízszint függvénye lehet. A felfelé szélesedő pezsgőspohár esetén például a pezsgő szintjének növekedésével erőteljesen nő a pohár kapacitása. Vagy egy másik gyakorlati példát említve, ha a Tisza elönti az árterületeket, nő a folyó kapacitása, mivel ugyanannyi hó beleolvadásakor nagyobb területen terül szét a hóból lett víz, így kevésbé emelkedik a Tisza szintje, amit jóleső érzéssel nyugtázhatnak a parti mércét aggódva figyelő szegedi polgárok.

A XVIII. században először a hő fluidumelmélete született meg.

Eszerint egy testbe beömlő hő mennyisége és a hőfok (ez felel meg a hő szintjének) emelkedése arányos egymással. Az arányossági tényező a test hőkapacitása. Képletben:

Q = C∙(T2-T1),
vagy még egyszerűbben
Q = C ∙∆T.

Itt Q a közölt hő mennyisége (latinul quantitása, ezért jelölik Q-val), T2-T1=∆T a hőfok emelkedése, C pedig a test hőkapacitása..

Az elmélet legnagyobb eredménye, hogy világosan megkülönbözteti egymástól a két legfontosabb fogalmat, a hő mennyiségét és a hő szintjét, vagy fokát. Ez utóbbit mondták a hő intenzitásának, illetve a hő mérsékletének is. Így keletkezett a hőmérséklet szavunk, és a latin temperatura kezdőbetűje lett a hőfok általánosan elfogadott jele.

Nem biztos, hogy jó választás volt erre a fontos fogalomra a mérséklet szót ráakasztani, de ma már senki se gondol a szó eredeti jelentésére. Úgy vagyunk vele, mint a vérmérséklettel, latinul temperamentummal, ennek hallatán se jelenik meg lelki szemeink előtt a mérséklet fogalma. Még leginkább a zenében, a “temperált skála” kifejezésben fedezhetjük fel e szó eredeti jelentését.

Senki se tudta a XVIII. században, hogy mi az a hőmennyiség. Mindenesetre megmaradó dolognak gondolták. A hő már a régi görögök elképzelése szerint is az egyik jellegzetesen imponderábilis mennyiség volt, vagyis olyan, aminek nincs mérhető súlya, illetve tömege. Mennyisége mégis van, ami viszont a hőkapacitás és a hőmérséklet-változás ismeretében meghatározható – mondták a XVIII. század fizikusai, miután feltalálták a hőmérőt, a hőmérséklet mérőeszközét.

A hő át tud áramlani egyik testről a másikra, amint a víz is átfolyhat egyik edényből a másikba. Közlekedőedényekben abból az edényből folyik át a víz a másikba, amelyikben magasabb a vízszint – egyensúly esetén pedig a szintek kiegyenlítődnek. A hő is abból a testből áramlik át a másikba – mondták –; ahol magasabb a hőszint, vagyis a hőmérséklet, s egyensúly esetén a hőmérsékletek kiegyenlítődnek.

Milyen szép és megkapó analógia!

El is terjedt a hő fluidumelmélete olyan sikeresen, hogy mind a mai napig él az emberek tudatában. Fourier erre, a hő fluidumelméletére alapozva dolgozta ki a XIX. század elején a hővezetés elegáns matematikai elméletét, amit mérnökök és vegyészek ma is előszeretettel használnak a mindennapi gyakorlatban. Lavoisier, a XVIII. század egyik legnagyobb kémikusa, aki pontos kísérleteivel és következetes gondolkodásával tudományosan megcáfolta az égés flogisztonelméletét, élete tragikus végéig hitt abban, hogy van hőanyag, és caloricum néven be is illesztette az általa ismert elemek közé, az oxigén mellé. Magyarországon még a XIX. század elején is jelent meg olyan tankönyv, amely Lavoisier nyomán, az ő tudományos tekintélyére hivatkozva vette fel a caloricumot a kémiai elemek sorába. A caloricum mértékegysége a kalória – orvosok és fogyni akaró hölgyek és urak mind a mai napig kalóriatáblázatok segítségével állítják össze betegeik vagy saját maguk számára a javasolt étrendet…

A hő fluidumelmélete mintájára, ugyancsak a XVIII. században született meg az elektromosság fluidumelmélete.

Az elektromosság is jól beleillett az imponderábiliák birodalmába: korabeli mérőeszközökkel lehetetlen volt kimutatni, hogy a dörzsöléssel elektromossá tett szigetelőrúdnak megváltozott volna a tömege a dörzsölés hatására. Miután Franklin szerencsés választással bevezette az elektromosság mennyiségére a töltés mennyisége kifejezést, már csak az elektromosság szintjére, fokára kellett egy szót kitalálni. Jelöljük ezt a mennyiséget egyelőre U-val, s írjuk fel a fluidumelmélet alapösszefüggését – az elektromosságra:

Q = C∙(U2-U1) = C∙∆U.

Itt tehát Q jelenti a testtel közölt elektromos töltés mennyiségét (érthető, hogy miért jelölik Q-val, ugye?), C a test elektromos kapacitása, U2-U1=∆U az elektromosság szintjének, fokának emelkedése a testben.

A fluidumelmélet tehát az elektromosságtanban is segített világosan elkülöníteni egymástól két alapfogalmat, az elektromosság mennyiségét és szintjét. Azokat a testeket, amik elektromossággal feltölthetők, amikben az elektromosság tárolható, elnevezték kondenzátoroknak. (Az elnevezés Voltától ered, aki ezzel a kondenzátor = sűrítő szóval azt akarta kifejezni, hogy ez az eszköz magába sűríti az elektromosságot, az elektromos töltést.)

Elég hamar rájöttek azonban arra, hogy az elektromos kapacitás nem egyedül a testre jellemző, mint mondjuk a test hőkapacitása, hanem erősen függ a test környezetétől. A legegyszerűbb elektromossá tehető test, egy sík fémlap esetén akkor válik ennek kapacitása egyértelművé, ha közelhelyezünk hozzá valamilyen megadott távolságra, vele párhuzamosan, egy másik, ugyanilyen fémlapot, amit vezetővel összekötünk a Földdel – más szóval “leföldelünk”. Hogy kerül ide a Föld? Úgy, hogy ennek kapacitása a laboratóriumi kísérletek szempontjából végtelen nagynak tekinthető.

A Földben az elektromosság szintje változatlan marad, akár töltést nyer, akár töltést veszít a Föld. Olyan ez, mint a tenger szintje a folyadékok számára: nem változik a tengerszint attól, hogy az ember valamennyi vizet beleönt a tengerbe, vagy kimer a tengerből. Ha tehát a két párhuzamos fémlemez egyikét leföldeljük, akkor ebben az elektromosság szintje mindig a Földével lesz egyenlő. Önkényes, de célszerű a Földben az elektromosság szintjét nullának választani és ehhez viszonyítani más testekben az elektromosság szintjét. Mint ahogy földrajzban is a tenger szintjéhez viszonyítjuk a hegyek magasságát.

Itt az ideje, hogy elnevezzük ezt az U-val jelölt mennyiséget, az elektromosság szintjét, még pedig – megállapodás szerint – a Földhöz viszonyított szintjét valaminek. Nos, legyen a neve elektromos feszültség.

Amikor manapság 150 kilovoltos távvezetékről beszélünk, ezt úgy értjük, hogy az elektromosság szintje a távvezetékhuzalokban százötvenezer volttal magasabb, mint az elektromosság szintje a Földben, vagy a földön álló távvezetékoszlopban. Ezért kell a huzalt a tartóoszloptól óriási porcelánszigetelőkkel elválasztani. Persze a huzal két pontja között is van feszültség, különben nem lenne, ami az áramot hajtja benne, de ez alig néhány volt kilométerenként. Az elektromos áram felfedezése és tulajdonságainak kipuhatolása azonban már a következő, a XIX. század tudósainak hozott dicsőséget, az emberiségnek pedig megadta a gazdasági fejlődés lehetőségét.

Térjünk vissza a XVIII. század elektromos fluidumelméletéhez. Eszerint fémtesteken az elektromosság a test felületén helyezkedik el és szintje a felület minden pontján ugyanaz. Két fémtest közötti feszültség a Földhöz képesti feszültségeik különbsége.

Egy kondenzátor feszültségéről nyilván akkor is beszélhetünk, ha egyik lemeze sincs leföldelve. Ilyenkor általában az egyik lemezen pozitív, a másikon negatív töltés van, a két töltés abszolút értéke egyenlő. A kondenzátorokra vonatkozó Q=CU közismert összefüggésben Q a lemezeken lévő töltések abszolút értékét, U pedig a lemezek közti feszültség abszolút értékét jelöli, C a kondenzátor kapacitása.

Elég érdekes, hogy a síkkondenzátor kapacitása arányos a lemezek területének nagyságával, ahogyan már említett példánkban a Tisza kapacitása is arányos az elöntött területekével, vagy még távolabbi példát véve: egy ország embereket befogadó képessége is arányos az ország területével.

Két XVIII. századi tudósról illik még megemlékeznünk, akik az elektromosság fluidumelméletét megalkották, s ezzel az elektromosságtan két legfontosabb alapfogalmát a töltést és a feszültséget egymástól elkülönítve tárgyalták.

Giovanni Battista Beccaria (1716–1781) itáliai piarista szerzetes volt, aki Franklin nyomán ásta bele magát igazán az elektromos kíséretezésbe. 1748-tól volt az egyetem fizikaprofesszora Torinóban. Az elsők között ismerte fel, hogy az elektromosság mindig a vezetők felületén helyezkedik el. Amikor megismételte Franklin kísérleteit, nemcsak sárkányt eregetett a zivatarfelhőkbe, hanem rakétát is fellőtt, ami vashuzalt húzott maga után.

1753-ban jelent meg Torinóban Dell’ elettricismo naturale ed artificiale (A természetes és mesterséges elektromosság) c. munkája. Két évvel Franklin után, 1755-ben őt is tagjául választotta a londoni Royal Society. Kutatási eredményeit, azok értelmezését korolláriumokba foglalva, latinul publikálta a Royal Society évenként kiadott hivatalos folyóiratában, a Philosophical Transactionsban.. Leghíresebb munkája még életében – 1778-ban – megjelent angolul is.

Henry Cavendish (1731-1810) gazdag családból származó angol fizikus és kémikus volt, aki saját laboratóriumában végezhette tudományos kísérleteit. 1753-ban, abban az évben fejezte be egyetemi tanulmányait Cambridge-ben, amikor az egész európai tudományos élet Franklin kísérleteitől volt “felvillanyozva”.

A maga örömére kísérletezett, kísérleteiről gondos feljegyzéseket készített, amikről be is számolt a Royal Society ülésein. Ott hamar felismerték a fiatal tudós tehetségét, elismerték eredményeit, és még nem volt 30 éves, amikor már a Royal Society tagjául választották. Publikálni azonban csak 1766-ban kezdett, természetesen a Philosophical Transactionsban.

Cavendishnek az elektromosság fluidumelméletével kapcsolatos legfontosabb publikációja 1771-ben jelent meg, a következő címmel: An attempt to explain some of the principal phenomena of electricity by means of an elastic fluid (Kísérlet az elektromosság néhány alapvető jelenségének értelmezésére egy rugalmas fluidum segítségével).

_________________________

1 A "2005 a Fizika Éve" című előadás-sorozat keretében Szegeden, 2005. április 4-én elhangzott előadás szerkesztett változata.

Természet Világa 2006. február - Tudománytörténet