Háromszáz évvel ezelőtt született minden idők egyik legéleseszűbb ("acutissimus") és legtermékenyebb matematikusa, Leonhard Euler, akit a világ nemcsak matematikusként, hanem fizikusként, mérnökként, csillagászként, filozófusként és pedagógusként is ismer.
Munkáit Eneström svéd matematikatörténész gyűjtötte össze és rendszerezte (1910). Az Eneström-index szerint Eulernek 866 műve jelent meg: egy napra átlagosan 15,5 oldal megírása jutott. A kéziratok közül körülbelül 200-at vakon készített el. Halála után még 47 év telt el, amíg hagyatékát fel tudták dolgozni. A matematikakönyveket úgy írta, mint Jókai Mór a regényeket. Félelmetes emlékezőtehetsége volt, ezért a matematika Mozartjának is hívták. Könyv nélkül tudta az Aeneist, egészen halála napjáig hiba nélkül idézte. Szentpétervári titkára, N. Fuss szerint egy éjszaka, amikor nem tudott aludni, megtanulta 1-től 100-ig a természetes számok hatványainak értékét egészen a hatodik hatványig, s a 600-nál több számból álló táblázat számait egy hét múlva is vissza tudta idézni. Bonyolult képletekre évtizedekig emlékezett. Mindent megjegyzett, amit elolvasott vagy hallott, így életének utolsó 15 évében, amikor már vak volt, nem okozott gondot a munka: mindent követett fejben. Elképesztően tudott számolni. Arago, a francia csillagász azt írta róla, hogy úgy számolt, ahogyan más lélegzett, vagy ahogyan a sas repül.
Összegyűjtött munkái, a Leonhardi Euleri Opera Omnia, 82 kötetben jelentek meg (1910-1998). Az első sorozatba a matematikai munkák tartoznak (Series I.: Opera mathematica, 29 könyv 30 kötetben). A második sorozatban mechanikai és csillagászati művei találhatók (Series II.: Opera mechanica et astronomica, 31 könyv 32 kötetben). A harmadik sorozatban fizikai tárgyú munkái és vegyes témák kaptak helyet (Series III.: Opera Physica, Miscelleanea 12 kötet). A negyedik sorozat A része (1975-1998) (Series IV. A: Commercium epistoloicum, 10 kötet) Euler levelezéseit tartalmazza. 3000-nél több levél található benne. A negyedik sorozat B része eddig még nem publikált Euler-kéziratokat, jegyzeteket és naplókat fog tartalmazni.
Eulert nemcsak a nagy munkabírás jellemezte, hanem az is, hogy családszerető és mélyen vallásos ember volt. Esténként a Bibliából tartott felolvasást családjának. Igen gondos apa volt, nem zavarta a körülötte zsibongó gyereksereg. Az anekdota szerint a vacsora két gongütése közti félórában Euler megfogalmazott egy matematikai tételt úgy, hogy egy gyerek a nyakában volt, egy másik a térdén lovagolt, a többiek a földön mászkáltak. Öt gyermeket nevelt fel, akik közül három fia (Johann Albrecht, Karl Johann és Christoph) neves ember lett. Szerette a zenét. Több nyelven is tudott (latin, francia, orosz, görög, keleti nyelvek), de a legjobban a régies svájci németet kedvelte. Matematikán és fizikán kívül sok mindennel foglalkozott. Készített horoszkópot Iván cárevics részére, szemüveget Nagy Frigyes porosz király számára, charlottenburgi birtokán pedig gazdálkodott.
Hol találkozhatunk Euler nevével?
Euler neve nem ismeretlen a XXI. századi középiskolások számára sem. Tanulmányaik során a geometriában előkerül az Euler-egyenes, az Euler- (Feuerbach-) kör, az Euler-féle poliéder tétel, a gráfelméletben a königsbergi hidak problémája, hallanak az Euler-féle "e" számról. Kevésbé ismert, hogy Eulertől származik a függvényfogalom egyik megfogalmazása (analitikus függvények), a szögfüggvények "sin, cos, tan, cot" jelölése. A "pi" jelölésére ő vezette be a p
-t, a 
imaginárius egység jelölésére az i-t, az összegzésre a
-t, a különbség jelölésére a D
jelet. Az ABC háromszög oldalhosszait a, b, c-vel való jelölte, amit ma is követünk az iskolában. Ő használta a R, illetve a r betűket a háromszög köré, illetve a háromszögbe írt kör sugarának a jelölésére, és a zárójelek különböző formáit is alkalmazta.
A tudományok fejlődése során számos esetben kapcsolódik össze egy fogalom egy tétel felfedezőjének a nevével.
Euler nevét megtaláljuk a következő elnevezésekben:
, e = 
, ex = 
;
;
(1/b ábra);
(2. ábra);
Euler élete
Gyerekkor és ifjúság
Édesapja, Paul Euler egy Bázelben letelepedett iparos családból származott. A bázeli egyetemen teológiát tanult, majd református papként szolgált a Bázelhez közeli Riehen parókiáján. Édesanyja, Margarethe Brucker református pap gyermeke volt. Négy gyermekük közül a legidősebb, Leonhard Euler 1705. április 15-én születetett Bázelben. Gyerekkorát Riehenben töltötte. Első tanítója édesapja volt, fia matematikai tudását ő alapozta meg. Paul Euler büszke volt arra, hogy Jakob Bernoulli (1655-1705) tanítványa lehetett. Leonhard szorgalmasan gyakorolt a nehéz matematikai könyvekből. Ezek egyike volt Coss könyve, egy elemi matematikakönyv, amely nagyon sok gyakorlati élettel kapcsolatos feladatot tartalmazott; ezek megoldása gyakran vezetett másod- vagy harmadfokú egyenletekre.
Euler 8 éves korában kezdte el gimnáziumi tanulmányait a bázeli hétosztályos gimnáziumban. A matematikaoktatás színvonala gyenge volt, ezért a szülők egy matematikában tehetséges fiatal teológust fogadtak mellé matematikatanárnak. Az Euler családnak jó kapcsolata volt a híres bázeli matematikus, Johann Bernoulli (1667-1748) családjával. Leonhard Euler az ő fiaival, Nikolausszal és Daniellel, elsősorban Daniellel kötött életre szóló barátságot.
Édesapja Leonhardot papi pályára szánta; 14 éves korában lett a bázeli egyetem filozófia fakultásának hallgatója. Közben szorgalmasan látogatta Johann Bernoulli előadásait, s a neves tanár felismerte tanítványa matematikai tehetségét. Matematikai könyveket adott neki tanulmányozásra, illetve szombat esténként megbeszélte vele a kiadott anyagot. Euler 14-15 éves korában két latin nyelvű tanulmányt is készített. Ezek egyike volt Az aritmetika és a geometria szónoklata (Declamatio de Arithmetica et Geometria, 1721) (3. ábra), amelyben latin nyelven fejtette ki, hogy a matematika milyen hasznos a gyakorlati életben. A 300 éves Euler-évfordulón az egyik bázeli kiállítás mottóját ebből a gyerekkori munkából választották ki. 1722-ben prima laurea kapta meg azt az akadémiai fokozatot, amely az érettséginek felel meg. 1723-ban Iselin mellett A római jog történetéről (Brevis Romanorum Judicorum Historia) értekezett (4. ábra). 1724-ban egy latin nyelvű nyilvános előadásban Descartes és Newton természetfilozófiai rendszerét hasonlította össze. 1724-ben befejezte az alapkurzust és megkapta a magiszteri fokozatot. Édesapja kívánságára beiratkozott a teológiára, de Bernoulli hatására az apa belátta, hogy fiának nem a papi pályán van a helye. Euler szeretett volna a bázeli egyetem fizika tanszékén állást kapni, de ez nem sikerült.
 | 
| |
| 3. ábra. Declamatio | 4. ábra. A római jogtörténetéről |
Első tudományos munkáiban (E1, E3) és habilitációs disszertációjában (E2), fizikai kérdéseket tárgyalt. A hajóárbocok legjobb elhelyezéséről szóló pályaművével (E4) második helyezést ért el a francia tudományos akadémia pályázatán.
A szentpétervári első periódus
(1727-1741)
1724-ben I. Péter cár megalapította a szentpétervári tudományos akadémiát, amelyet 1726-ban nyitottak meg. 1725-ben Nikolaus és Daniel Bernoullit meghívták Szentpétervárra professzornak. Daniel távozásakor megígérte barátjának, hogy ha nem tud Bázelben elhelyezkedni, segíteni fog egy szentpétervári állás megszerzésében. Ez sikerült is. Az anatómiai és élettani tanszéken volt egy üres adjunktusi állás. Euler elfogadta az ajánlatot.
1727 tavaszán megérkezett Szentpétervárra. Nem volt kétségbe esve attól, hogy orvosi problémákkal kell foglalkoznia. Élettani kutatásai során a vérkeringés hidrodinamikai problémáit vizsgálta, és ezzel a hidrodinamika tudományának létrejöttét segítette elő.
1730-ban meghalt II. Péter cár. A helyzet bizonytanná vált, és a tudósok egy része eltávozott Oroszországból. Euler a megüresedett matematika tanszék, majd Daniel Bernoulli távozása után a fizika tanszék professzora lett.
Élete összeforrt a szentpétervári akadémiával, és 50 éves munkássága alatt az akadémia egyik legjelentősebb személyévé vált. 1734-ben a szentpétervári akadémia elnöke lett. Szorgalmasan dolgozott, részt vett a mértékrendszer reformjának elkészítésében, előadott az akadémiai konferenciákon, számtankönyvet írt az akadémiai gimnázium számára, ismeretterjesztő cikkeket jelentetett meg. Szoros kapcsolatba került Goldbachhal. Ez a kapcsolat szakmailag különösen fontos volt a számára. 1733-tól térképek ellenőrzésében vett részt, ami nagyon igénybe vette a szemét. 1735-ben többször volt igen magas láza, a korabeli leírások elemzése alapján görvélykórban (scrophulosis) szenvedhetett, aminek következtében elvesztette jobb szemének világát - így abbahagyta a szemet megerőltető térképészeti vizsgálatokat. 1740-ben egészségi állapota tovább romlott.
Az orosz belpolitikai helyzet is igen feszültté vált, ezért kérte az akadémiától az elbocsátását. Az akadémia tiszteletbeli tagjaként távozott 1741-ben Berlinbe, elfogadva II. Frigyes porosz király meghívását.
Tudományos munkássága 1727 és 1741 között
Euler Szentpéterváron lett nagy matematikussá. 53 munkája (E5 - E57) készült el. Ekkor született első nagy monográfiája, a Mechanika, azaz a mozgástudomány analitikus módon kifejtve (Mechanica, 1736, E15). Eulerig kevés mechanikával foglalkozó munka alkalmazta a matematika infinitezimális számítási módszereit. A mechanikát Euler emelte egzakt tudománnyá. Az általa bevezetett jelöléseket ma is használják, az általa tárgyalt feladatok egy része ma is változatlanul található meg a fizika tankönyvekben.
A mechanikán kívül több témakörrel foglalkozott:
Euler berlini évei
(1741-1766)
Euler II. Frigyes szolgálatára érkezett Berlinbe, ahol 25 évet töltött. Első feladata a berlini tudományos akadémia megszervezése volt. 1740-ben Leibniz megalapította a brandenburgi Tudományos Társaságot. 1743-ban Euler tervei szerint az akadémián négy osztályt akartak létrehozni, de a filozófiai osztály nem valósult meg. 1744-ben a matematikai osztály megalapítója és első igazgatója Euler lett, az elnöke Maupertuis, az európai hírű professzor. Euler tagja volt a londoni és a francia tudományos akadémiának.
Euler széles körű műveltséggel rendelkezett, sok mindenhez értett, sok gyakorlati kérdéssel foglalkozott. Ő ellenőrizte a Havelt és az Oderát összekötő Finow-csatorna szintezési munkáit, a schönebecki sólepárló üzemek állapotát, tanácsot adott az állami lottójáték megszervezésére. Részt vett a Sanssouci-park szökőkútjainak tervezésében, de ezzel a munkájával Nagy Frigyes nem volt megelégedve. Kikérték javaslatát a hallei egyetem megüresedett matematikaprofesszori székének betöltéséről.
1753-ban nagy összeget nyert a lottón: ebből vette meg charlottenburgi a birtokát, de Schönefeldben is volt gyümölcsös kertje.
 |
| |
| 5. ábra. A maximum- és
minimum-tulajdonságú görbék feltalálásának módja | 6. ábra. Bevezetés a végtelenek analízisébe |
Euler tudományos munkássága a berlini évek alatt (1741-1766)
Euler berlini tartózkodása alatt publikálta E46-321 munkáit. A berlini években elért tudományos eredményei alapvetők, például majdnem hiánytalanul bebizonyította az algebra alaptételét. 1744-ben jelent meg híres könyve, A maximum- és minimum-tulajdonságú görbék feltalálásának módja (Methodus invenienendi lineas curvas, E65)
(5. ábra), amelyben a maximum- és minimum-problémákkal foglalkozott. Az izoperimetrikus problémákon kívül gyakorlati problémákat tárgyalt. A variációszámításban alkalmazta a differenciálást. A minimál-törvényt, a legkisebb hatások elvét helyesen fejtette ki.
7. ábra. A differenciálszámítés alpjai
Nagy Frigyest nagyon érdekelték a tüzérségi problémák, és Eulernek az angol Benjamin Robins A tüzérség új alapelvei című munkájával (1742) kapcsolatban tett fel kérdéseket. Euler azt javasolta, fordítsák le ezt a könyvet németre. Fordítás közben észrevette, hogy sok hiba van benne, ezért teljesen átdolgozta, felhasználva benne az analízis módszereit (differenciálás, integrálás). A könyv (1745, E77) igen jó lett. Lefordították angolra, illetve franciára. A francia tüzérségi iskolában azonnal bevezették tankönyvként. Valószínűleg Napóleon is ebből tanult.
Ebben az időszakban jelentek meg matematikából a Bevezetés a végtelenek analízisébe (Introductio in analysin infinitorum, 1748, E101) (6. ábra) és a Bevezetés a differenciálszámításba (Institutiones calculi differentialis, 1755, E212) című könyvei (7. ábra).
Maupertuis 1759-ben meghalt. Euler arra számított, hogy ő fogja megkapni az akadémia elnöki tisztét. A francia műveltséghez kötődő király viszont másképpen döntött, az Eulernél 10 évvel fiatalabb D’Alembert-t kérte fel erre a tisztségre és az Eulerénél jóval magasabb fizetést ajánlott fel neki. Euler és Nagy Frigyes között egyre romlott a viszony. Lassanként megérlelődött Eulerben a távozás gondolata. Szülőföldjére nem tért vissza. Nem tartott igényt a Johann Bernoulli halálával (1748) megüresedett bázeli professzori állásra sem. Oroszországban azonban rendeződtek a körülmények.1766-ban megérkezett II. Katalin cárnő meghívója.
A szentpétervári második periódus
(1766-1783)
II. Katalin cárnő igen jó feltételeket ígért. Euler számára létrehozta a szentpétervári tudományos akadémia alelnöki tisztségét, és megbízta őt az akadémia átszervezésével. Sajnos, Euler látása egyre romlott. Egyik szeméről eltávolították a szürke hályogot, de ismét megvakult. Tudományos munkáját nem szakította félbe. Először egy nagy fekete asztalra írta rá krétával számításait, amelyeket tanítványai (elsősorban Fuss) egy nagy könyvbe írtak be, és később cikkeket állítottak össze belőlük. Hasonlóan segítségére volt fia, Johann Albrecht, illetve munkatársai közül Lexell és Kraft.
76 éves korában halt meg agyvérzésben. Halálának napján még foglalkozott unokájával, majd Fuss-szal és Lexell-lel az akkor felfedezett Uránusz bolygó pályáját számolták.
Euler tudományos munkássága 1766 és 1783 között
A második szentpétervári periódus alatt jelent meg két szenzációs bestseller könyve: Levelek egy német hercegnőhöz (Lettres à une princesse d’Allemagne sur divers sujets de physique & de philosophie, 1768, E343) (8. ábra) és a Teljes bevezetés az algebrába (Vollständige Anleitung zur Algebra, 1770, E387) (9. ábra). Ekkor írta a háromkötetes Bevezetés az integrálszámításba (Institutionum calculi integralis, 1768-1770, E342) (10. ábra), a kétkötetes Optika (1769, E367), a Hold mozgásának elmélete (1772, E418) és a kétkötetes Hajóépítés (1773, E426) című monográfiáit. Az utóbbi mű óriási sikerét mutatja, hogy a francia király azonnal kötelező anyaggá tette a hajózási iskolában, Katalin cárnő pedig oroszra fordíttatta le.
|
8. ábra. Levelek egy német hercegnőhöz |
9. ábra. Teljes bevezetés az algebrába |
10. ábra. Az integrálszámítás | alapjai |
 |
 |
 |  |
Euler barátai és szakmai kapcsolatai
A Bernoulli testvérek: Daniel és Nikolaus
Daniel Bernoulli (1700-1782) svájci matematikus, Johann Bernoulli (1667-1748) kisebbik fia. Orvosnak készült, de a későbbiekben elsősorban fizikával foglalkozott. Eulerrel még ifjúkorában, Bázelben ismerkedett meg és kötött szoros barátságot. 1725 és 1733 között Szentpéterváron volt az akadémia fizikaprofesszora. Svájcba való visszatérése után Euler az ő helyét foglalta el. Daniel Bernoulli a folyadékok nyomásával és dinamikájával foglalkozott, az ő nevét viseli a folyadékok áramlásának Bernoulli-törvénye. Leghíresebb munkája az 1738-ban kiadott Hidrodinamika című könyve. Eulerrel együtt vizsgálta a rezgő húrokat. Sok eredménnyel gazdagította a valószínűség-számítást is.
A Bernoulliak (Johann, Jakob, Daniel) tanítványa volt Bázelben a Debreceni Református Kollégium híres professzora, Hatvani István is. Így érthető, hogy a Debreceni Református Kollégium Nagykönyvtárában az egyik Bevezetés az algebrába (1771) könyv Stephanus Hatvani tulajdona volt.
Nikolaus Bernoulli (1695-1726), Daniel Bernoulli bátyja szintén matematikus volt. Daniellel együtt ment Szentpétervárra 1725-ben, de néhány hónap múlva meghalt. Differenciálegyenletekkel és valószínűség-számítással foglalkozott. Ő vetette fel a valószínűség-számítás egyik nevezetes problémáját, az ún. pétervári paradoxont.
Segner János András (1704-1777)
Ő az első, elismert, magyar származású matematikus, akit a nemzetközi matematikatörténet is számon tart. Pozsonyban született; Győrben, majd Debrecenben is tanult egy évig. Utána Jénában járt egyetemre. 1730-ban Debrecen tisztiorvosa lett. 1732-től már Jénában, majd Göttigenben és Halléban volt professzor. Foglalkozott matematikával (Descartes-féle jelszabály), mechanikával, optikával, hangtannal. Több könyve jelent meg. Ő is felfedezte a Cavalieri-elvet. Nevéhez fűződik a Segner-kerék, vagyis a turbina ősének megszerkesztése. E témában együttműködött Eulerral. Segner és Euler 30 évig levelezett egymással (1741-1771); a feljegyzések 159 darab, Segner által írt levelet tartanak számon, Euler 17 levelet írt.
A göttingeni csillagvizsgáló igazgatói székéért folyó, Segner és Tobias Mayer közti vita lezárásában nagy szerepe volt Eulernek, aki 1751 és 1755 között együtt dolgozott Tobias Mayerrel a Hold-táblázatokon. Euler jó viszonyban lehetett a nehéz természetű Segnerrel. Erre utal, hogy 1763-ban fiával nála szállt meg. Meg kell említeni, hogy a hallei egyetem Ch. Wolff halálával megüresedett professzori székébe Euler javaslatára nevezték ki Segnert professzornak, miután Daniel Bernoulli nem fogadta el az állást.
Tobias Mayer (1723-1762)
Göttingeni professzor, aki matematikus, fizikus, csillagász és térképkészítő volt.
Könnyen összetéveszthető fiával, Johann Tobias Mayerrel (1752-1830), aki szintén göttingeni matematikus és fizikus professzor volt, a Királyi Tudományos Akadémia tagja. Tobias Mayer árva volt. Matematikai ismereteit autodidakta módon sajátította el, és nagyon fiatalon továbbadta munkáiban. Első könyvét 18, második könyvét 22 évesen írta. Ez utóbbi a Matematikai atlasz (Mathematischer Atlas, Augsburg, 1745), amelyből a német szakirodalom nyolcat tart számon; a kilencedik, színezett példány a Debreceni Református Kollégium Nagykönyvtárában található (R72, O351).
Mayer csillagászati kutatásainak eredményeit Euler az elméleti csillagászat csodálatos mesterművének nevezte. Tobias Mayer posztumusz kiadású Theorie lunae juxta Systema Newtoniam (London, 1767) és Tabulae mutiu solis et lunae novae et correctae (London, 1770) munkái Euler számításaira támaszkodtak és a tudományos navigáció alapját képezték. A Tobias Mayer által készített ismétlő (recipiens) körző felhasználásával a hajók pontos tartózkodási helyét, vagyis a hosszúsági fokot, meg lehetett határozni a tengeren. Az angol parlamenttől Tobias Mayer özvegye 3000, Euler pedig 300 fontot kapott ezért az eredményért. Euler a későbbiekben is foglalkozott a Hold fázisaival, más égitestekkel és az üstökösök elliptikus pályájának kiszámításával. Vizsgálta a Lexell-üstököst, amely 1769-ben, majd 1983-ban közelítette meg a Földet.
Euler munkái
Euler minden munkájának alapja a matematika volt. Filozófiai elvet követett, az elméletből kiindulva akart eljutni a gyakorlatig. Úgy gondolta, hogy a természettudományos felfedezésekhez néhány általános, megkérdőjelezhetetlen alapelv elméleti, elsősorban matematikai vizsgálata útján lehet eljutni. Így mind a mechanikában, mind a csillagászatban elért eredményei a matematikai módszerek alkalmazásához kapcsolódtak. Matematikából a következő témakörökkel foglalkozott: algebra0, számelmélet, geometria, trigonometria, kombinatorika, valószínűség-számítás, az analízis alapjai, differenciál- és integrálszámítás, végtelen sorok, differenciálegyenletek és -egyenletrendszerek, variációszámítás, iskolai matematika.
Legfontosabb matematikai eredményei
Számelmélet
Euler volt az a matematikus, aki megteremtette az általános számelméleti kutatásokat. Számelméleti problémákkal Szentpéterváron találkozott, ahol Goldbachtól (1690-1764) értesült Fermat (1601-1665) munkásságáról és levelezett is vele erről a témáról. Goldbach az 1742-ben Eulerhez írt levelében azt állította, hogy minden 3-nál nagyobb pozitív egész szám előállítható három prímszám összegeként. Euler válaszlevelében kifejtette, elegendő azt megmutatni, hogy minden páros szám felbontható két prímszám összegére. Ezt az állítást nevezik Goldbach-sejtésnek és a mai napig nem sikerült bebizonyítani.
Fermat azt állította, hogy minden Fn = 
+ 1 alakú szám prímszám minden n pozitív egész szám esetén. Valóban, F0 = 3, F1 = 5, F3 = 257, F4 = 65537 prímszám. .Euler 1732-ben megmutatta, hogy F5 = 232 + 1 = 641×
6700417, vagyis osztható 641-gyel, már nem prímszám. Ma k =19-ig van kimutatva, hogy Fk nem prím; nem ismert, hogy van-e még Fk prímszám a nagyobb k értékekre.
Euler a Mersenne- (1588-1648) prímszámokat is vizsgálta. A Mersenne-féle prímszámok alakja: Mp = 2p -1, ahol p prímszám. Euler azt látta be, hogy M31 = 2147483647 prímszám. Ma számítógépek segítségével végzik a számításokat. 2006-ban az ismert legnagyobb Mersenne-féle prímszám: 232582657-1.
A Mersenne-féle prímszámokhoz az ún. tökéletes számok vizsgálatakor lehet eljutni. Tökéletes számnak nevezzük azt a pozitív egész számot, amely egyenlő pozitív osztóinak az összegével, ha az osztók közé nem vesszük be magát a számot. Tökéletes szám például a 6, mert 6 = 1+ 2 + 3. Euler kimutatta, hogy az összes páros tökéletes szám alakja: 2n·(2n+1-1), ahol 2n+1-1 prímszám. Megmutatta, hogy n = 30 esetén tökéletes számot kap: 230· (231 -1).
Megtalált 61 barátságos számpárt is. Barátságos számpárnak nevezzük azokat a pozitív egész egészekből álló számpárokat, amelyeknél a két szám bármelyike egyenlő a másik szám valódi osztóinak az összegével; az 1-et beleszámítjuk az osztók közé, de magát a számot nem.
Fermat azt állította, hogy minden 4k + 1 alakú prímszám két négyzetszám összege, és ez az előállítás egyértelmű. Euler kimutatta, hogy a 4k + 3 alakú számok nem írhatók fel ilyen módon. 1749-ben megmutatta, hogy ha (a,b) = 1, vagyis ha a és b relatív prímek, akkor a2 + b2 nem osztható 4k - 1 alakú számokkal (kÎ N). Foglalkozott az állítás megfordításával is, ami a kvadratikus maradékok vizsgálatához vezetett el.
Euler igazolta a kis Fermat-tételt, amely kimondja, hogy ha p prím, és az a szám nem osztható p-vel, akkor ap-1 osztható p-vel. Utána bebizonyította a tételnek az összetett számok esetére való általánosítását. Ehhez felhasználta az ún. Euler-féle j -függvényt. Euler ezzel egy új típusú függvényosztályt teremtett meg, a számelméleti függvényeket. Ennek a függvénynek nagy jelentősége van egy n pozitív természetes szám osztói számának a meghatározásában.
Fermat híres sejtése volt a nagy Fermat-tétel, vagy mai nevén Fermat utolsó tétele, ami azt mondja ki, hogy az xn + yn = zn (nÎ N) egyenletnek nincs megoldása a pozitív egész számok körében, ha n>2. A tételnek n = 2 esetén a püthagoraszi számhármasok a megoldásai [pl. (3, 4, 5), (5, 12, 13), (7, 24, 25) stb.]. Euler n = 3, 4 esetére bizonyította be Fermat sejtését. A tétel bizonyítását Wiles angol matematikus adta meg 1995-ben.
Euler foglalkozott még az ún. Pell-féle egyenletekkel is. Kutatásainak jellemzője volt, hogy - nagyon jó számolási készségét kihasználva - rengeteg konkrét esetet számolt ki; 10 000-ig vizsgálta meg az összes számot. A vizsgálatok még ma sincsenek lezárva.
Euler további érdeme, hogy megalkotta az analitikus számelméletet, vagyis bevezette az analízis módszereit a számelméleti kutatásokban. Megállapította, hogy az egész számok természetének vizsgálatában hasznos eszköz a végtelen kicsi mennyiségekkel való számolás és a differenciálás. Sokat foglalkozott a számok feldarabolásával (partíciójával), vagyis azzal, hogyan és hányféleképpen lehet a természetes számokat bizonyos típusú összeadandók összegeként különböző módon előállítani. A generátorfüggvény-módszer segítségével bizonyította be Lagrange-nak azt a tételét, hogy a természetes számok 4 négyzetszám összegeként állíthatók elő és megadta az ilyen előállítások számát.
Analízis
Az infinitezimális számítás, vagyis a kalkulus területén az első lépéseket Leibniz és Newton tette meg. Munkáikban sok volt a hiányosság, ezeket vette észre Euler. A Bevezetés a végtelenek analízisébe című könyvében felépítette a függvényelméletet. Euler függvényfogalma egyrészt szűkebb volt, mint a mai függvényfogalom, mert az analitikus függvényekre szorítkozott, másrészt bővebb volt, mert többértékű függvényeket is magában foglalt, amelyeket ma már nem sorolunk a függvények közé. A későbbiekben terjesztette ki vizsgálatait a számelméleti függvényekre. Tőle származik az f függvény x helyen vett helyettesítési értékének f(x)-szel való jelölése.
Az első kötet csodálatos tankönyv, amely mindent tartalmaz, ami az analízis elsajátításához szükséges. Tárgyalja a függvény definícióját, a függvények osztályozását, átalakítását, szorzattá bontását és a helyettesítést. Megtaláljuk benne az elemi függvények, a logaritmus, az exponenciális, a trigonometrikus függvények és azonosságok középiskolai tárgyalását. A feladatok bármelyike szerepelhetne egy mai középiskolai tankönyvben. Az az egyetlen különbség, hogy a logaritmust "l" betűvel jelöli. A hatványozást negatív számra a következőképpen értelmezte: például
, ami képzetes és 
, ami valós. Kiterjesztette a logaritmusok elméletét a képzetes értelmezési tartományokra.
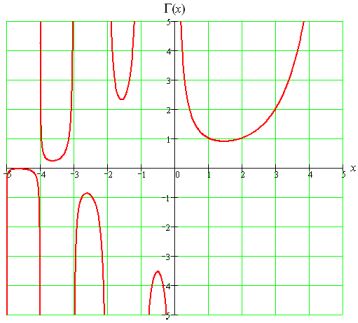
A könyvben megtaláljuk a végtelen sorok elméletét, az ex, sinx, cosx hatványsorait és a képzetes értékekre való kiterjesztését. Itt írja le a z (2n) kiszámítását.
Euler tette meg az első lépéseket a komplex analízis felé. Leghíresebb komplex analízisbeli eredménye az exponenciális és a trigonometrikus függvények közötti ún. Euler-formula: eix = cosx + isinx, amelyet Lagrange (1736-1813) az analízis egyik leggyönyörűbb felfedezésének tarotott, míg Feynman Euler drágakövének nevezte az előbbi formula speciális esetét, vagyis azt, hogy
.
11. ábra. Görbék
A könyv második része tartalmazza a koordinátageometriát, az általános görbe- és felületelméletet - nagyon sok ábrával. Foglalkozik a másodfokú (ellipszis, hiperbola, parabola) és a harmadfokú görbékkel
(11. ábra).
Ha Euler tanítási módszerét vizsgáljuk, megállapíthatjuk:
Minden általános definícióhoz ad konkrét példát. Van, amikor az általános fogalmat közli elsőként, de van, amikor a konkrét példa előzi meg az általános fogalmat.
Mindenre ad konkrét példát, az eljárásokat sok példán keresztül mutatja be, teszi érthetővé, utána általánosít.
Szereti a táblázatos összefoglalást, akár fogalmakról, akár adatokról van szó.
Gondosan előkészíti a későbbi feladatok matematikai alapjait. Ez jól látszik például a parciális törtekre való bontásnál. Ez utóbbi végrehajtása teljesen megegyezik a mai gyakorlattal.
A könyv kapcsán ki kell térnünk az ún. bázeli problémára.
A bázeli probléma
A bázeli probléma a négyzetszámok reciprokai végtelen sora összegének a meghatározása. A problémát Pierre Mengoli vetette fel a XVII. század közepén. Jakob Bernoulli első bázeli disszertációjában számos hasonló sor összegét határozta meg, de problémát jelentett számára az 1 + 1/4+ 1/9+… végtelen sor összegének megadása. 1691-ben megállapította, hogy az összeg nem lesz racionális. 1736-ban Eulernek sikerült megmutatnia, hogy
Euler a formulával új jelentést adott a természetes számokból felépített sorokra, az analízis eszközeit alkalmazta a számelméletben, és ezzel megalkotta az analitikus számelméletet.
A z
(s) = 1 + 
végtelen sor összegét is vizsgálta. Megtalálta, hogy az összeg szorzattá alakítható:
z
(s) =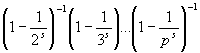 
.
A harmonikus sorok megfigyeléséről (De progressionibus harmonicis observationes, 1740, E43) dolgozatában született meg a z - (zéta) függvény és a γ. Ekkor vezette be a S jelet is.
Vizsgálta a H = 1 + 
harmonikus sort is, ami divergens. Ennek egy részletösszege:
.
Észrevette, hogy Hn - ln n »
0,577216 = C, konstans. Ezt ma Euler-konstansnak nevezzük és γ-val jelöljük:
γ.Euler úgy gondolta, hogy γ egy másik fontos szám logaritmusaként fejezhető ki. Több közelítési módszert is megadott. Páros kitevőkre oldotta meg a zéta-sorozatok összegzését. Páratlan kitevőkre a probléma ma is nyitott. Ezek a vizsgálatok a prímszámok számának végtelenségével függnek össze. A zéta-függvény új függvényelméleti szemléletmódot hozott. A komplex számok halmazára való kiterjesztése vezetett el a Riemann-féle sejtéshez, ami ma is megoldatlan probléma. A prímszámeloszlás átláthatatlansága igen fontos szerepet játszik az elektronikus adatátvitelnél és a kódolási rendszerekben. Ma sem bizonyított, hogy γ irracionális vagy racionális szám.
Érdekes Euler véleménye a prímszámokról (1751, commentatio 175): "A matematikusok hiába kutattak, hogy fel tudjanak fedezni valami rendszert a prímszámok sorozatában, és jó alapja van annak, hogy azt higgyük, ez misztérium, amit sohasem fog az emberi agy megérteni. Ahhoz, hogy erről meg tudjunk győződni, elég szemeinket a prímszámok táblázatára vetni: néhány ember vette a fáradságot és 100 ezrekig számolt, hogy sorba állítsa őket, és nem látott benne semmi törvényt. A legmeglepőbb ebben az aritmetikában az, hogy sok olyan biztos szabállyal látott el bennünket, amelyek segítségével ilyen számok sorozatát folytathatjuk olyan messzire, ahogy elképzeljük, de anélkül, hogy valami nyomát találnánk a szabálynak."
A Bevezetés a végtelenek analízisébe című könyvét a Differenciálszámítás tankönyve követte, amelyben a véges differenciákat, a magasabb rendű számtani sorozatokat, a differenciál alkalmazásait, az egy-, két- és többváltozós függvények többszörös differenciálását, a differenciálformulákat és a differenciálegyenleteket tárgyalta. Kitért a végtelen sorok alkalmazásaira, a sorok összegének keresésére, a függvények maximumának és minimumának megkeresésére. Nagyon sok kidolgozott példa található a könyvben - olyanok, amelyek még ma is szerepelnek a tankönyvekben és a példatárakban. Ilyen például az f(x) = 
függvény vizsgálata, szélsőértékeinek megkeresése. Foglakozott az implicit függvények differenciálásával, az interpolációval, az egyenletek valós gyökének megkeresésével és az imaginárius gyök létezésének kritériumaival. Megtalálta a differenciálegyenletek fizikai alkalmazásait a hidromechanikában, a húrok és membránok rezgéseinek, a hang terjedésének leírásában, a hullámegyenletben. Munkája nyomán a mechanika feladatai is átalakultak matematikai feladatokká, differenciálegyenletek megoldásává.
A háromkötetes Integrálszámításban is először az alapokat tárgyalta, majd az integrálási szabályokat, a szokásos racionális és irracionális, exponenciális, logaritmikus, trigonometrikus formák integrálását, a végtelen sorok integrálását, a parciális integrálást, az integrálást multiplikátorral és a differenciálegyenletek megoldását a mai gyakorlatnak megfelelően.
A harmadik kötet tárgya a Johann I. és Jakob Bernoulli által bevezetett variációszámítás. A variációszámítás segítségével számos gyakorlati probléma is megoldható. Ezen az elméleten alapul például a hajó és a repülőgép, a vasúti és autópályák íveinek az építése, a mesterséges szívbillentyű alakjának tervezése. Euler analízisbeli monográfiái összefoglalták a XVIII. századi matematikai felfedezéseket és azok gyakorlati alkalmazásait. Nagy hatást fejtettek ki a következő évszázadok tankönyveire és matematikai képzésére.
Geometria
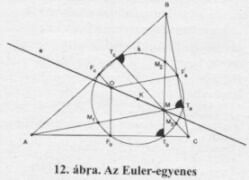Euler geometriai munkássága egyrészt elemi jellegű, másrészt a felsőbb geometria tárgykörébe tartozik. Elemi tételei a háromszögek és a sokszögek geometriájával kapcsolatosak. Ő írta le, hogy a háromszög magasságvonalai egymást egy pontban metszik, és ő mutatta ki, hogy a háromszög magasságpontja, körülírt körének középpontja és a háromszög súlypontja egy egyenesre illeszkedik, amit ma Euler-egyenesnek nevezünk
(12. ábra). Ő fedezte fel a háromszög Euler-körét, amit ma 9 pont körének, vagy Feuerbach-körnek nevezünk. Ő vezette be a p
jelölést a kör kerületének és átmérőjének arányára (1739).
Az ő nevéhez fűződik a háromszögekre vonatkozó Euler-tétel: d2 = R(R - 2r), ahol R a háromszög köré, r a háromszögbe írható kör sugara és d a háromszögbe és a háromszög köré írt kör középpontja közötti távolság. Az 1748-ban Goldbachhoz írt 125. levelében találunk egy addig nem ismert elemi geometriai tételt (13. ábra). Megemlíti, hogy a paralelogrammákra érvényes tételhez hasonló tételt talált a négyszögekre. Ez a következő: Legyenek az ABCD négyszög AC és BD átlóinak M és N a felezőpontjai. Ekkor AB2 + BC2 + CD2 + DA2 = AC2 + BD 2 + 4 MN2.
Az Euler-féle poliéder-tétel
A poliéderekkel Descartes (1596-1650) is foglakozott és elég közel került az Euler-tételhez. Euler A testek elemi doktrinája (Elementa Doctrinae Solidorum, 1758, E230) című cikkében mondta ki a poliéder-tételt, de részleteit megtaláljuk az 1750. november 14-én Goldbachhoz írt levelében is. Euler az állításra példákon keresztül jött rá, de általános bizonyítást először nem sikerült adnia, csak a Síkok által bezárt testek néhány tulajdonságának a bizonyítása (Demonstratio Nonnullarum Insignium Proprietas Quibus Solida Hedris Planis Inclusa sunt Praedita, 1758, E231) cikkében írta le. A poliéder-tételre a maihoz hasonló bizonyítást Cauchy adott 1813-ban.
Euler eredeti problémája a poliéderek osztályozása volt. Míg a síkgeometriában a sokszögek nagyon könnyen osztályozhatók az oldalak száma szerint, amely természetesen egyenlő a szögek számával, addig a térgeometriában nehezebb a poliéderek osztályozása, mert nem elegendő a lapok számának ismerete. Euler érdeme, hogy felfedezte a csúcs és az él fogalmát. Ő mutatta ki először a poliéderek topológiai jellegét. A régi latin latus (oldal) helyett az acies (él) fogalmát és elnevezését alkotta meg. A pontszerű csúcsok jelölésére meghagyta az angulus solidus (szilárd szög) fogalmat. A tétel kimondja: minden poliéderre igaz, hogy a lapok és a csúcsok számának az összege 2-vel több, mint az élek száma: c + l = e + 2, vagy c + l - e = 2 .
Az utóbbi forma általánosítható zárt felületekre. A 2 szerepét az Euler-karakterisztika (Euler-Poincaré-tétel) veszi át, de ez már a kombinatorikus topológia témakörébe tartozik. Későbbi cikkei is kapcsolódtak ehhez a témához (E309, E530).
Érdekesség, hogy az Euler-féle poliéder-tétel tárgyalását kapta meg doktori disszertáció témájaként Lakatos Imre Pólya Györgytől. Ebből a vizsgálatból született meg a Bizonyítások és cáfolatok című könyv és a Lakatos-féle heurisztika.
A königsbergi hidak problémája
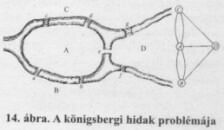A gráfelmélettel kapcsolatos a königsbergi hidak problémája. Ez a probléma ma a következőképpen van benne a középiskolai matematika-tankönyvekben
(14. ábra): "Königsberg a Pregel folyó két partján és két szigeten terül el. A térképvázlaton az A, B, C és D városrészeket hét híd (a, b, c, d, e, f, g) köti össze. A königsbergiek tervezhetnek-e olyan sétát, hogy otthonról elindulva és oda visszatérve minden hídon pontosan egyszer haladjanak át?"
1736-ban Marioninak írt levelében említi Euler először, hogy felvetettek neki egy feladatot arról a szigetről, amely Königsberg városában található, és amelyen az őt körülvevő Pregel folyón hét híd ível át. A feltett kérdés az volt: bejárhatja-e valaki a szigeteket úgy, hogy minden hídon csak egyszer megy át? A tapasztalat szerint ez lehetetlen volt, de ezt senki sem bizonyította be.
A kérdés Euler számára érdekesnek látszott, és megállapította, hogy megoldásához nem elegendő sem az algebra, sem a geometria, sem a kombinatorikus művészet. Úgy gondolta, a feladat a helyzetgeometriához tartozik, amelyet Leibniz említett meg 1679-ben. Ezzel felismerte a geometria egy új területének a szükségességét, egy olyan területét, amely nem tartalmaz méréseket. 1736 áprilisában Danzigba írt levelében igen érdekesen fogalmazott: "A megoldásnak kevés köze van a matematikához, és nem értem, miért kellene ennek megoldását inkább matematikustól várni, mint bárki más emberfiától. Ez a megoldás ugyanis kizárólag egy észrevételen alapul, és ahhoz, hogy megkapjuk, nincs szükségünk semmilyen speciális matematikai törvényre."
Lóugrások a sakktáblán
Euler jól sakkozott. Philidor Londonban megjelent sakk-könyvét (1749) tanulmányozta. 1757. április 26-i, Goldbachhoz írt levelében vázolta fel a "lóugrások problémájá"-t. A kérdés az volt, hogyan futhatja be a sakktábla mind a 64 mezőjét egy huszár úgy, hogy minden mezőre csak egyszer lép?
A probléma megoldására Euler talált egy sikeres módszert. A megoldás lényege az, hogy a sakktábla mezőihez számokat rendelt hozzá, mégpedig úgy, hogy az utolsó lépésnél a huszár a 64-es mezőről az 1-esre ugorjon. A feladatnak több megoldása is van. Észrevette, hogy a szemben fekvő mezők szimmetrikusak és a rajtuk levő számok különbsége 32 (15. ábra). Euler későbbi cikkei is kapcsolódtak ehhez a témához (E309, E530).
Ennek a problémának szintén van magyar vonatkozása. Euler feladatával Kürschák József foglalkozott és általánosította a végtelen sakktáblára. A lóugrások problémája megoldásának modernebb változatában az egymás után következő számokat szakaszokkal kötjük össze. Ekkor egy gráf Hamilton-vonalának speciális esetét kapjuk.
A két besteller könyv
Levelek egy német hercegnőhöz
1760 és 1762 között a brandenburgi herceg kérésére Euler ranciául írta meg a Leveleket a herceg 15 éves lánya számára, aki Nagy Frigyes unokahúga volt. A könyv népszerű formában tartalmazza a XVIII. század közepének fizikai, filozófiai, logikai, ismeretelméleti, etnikai és teológiai ismereteit. Az eredeti francia kiadás 1768-ban jelent meg Szentpéterváron. Később lefordították német, orosz, holland, svéd, olasz nyelvre. Körülbelül 40 kiadása jelent meg, korának bestsellere volt. Debrecen régi könyvtáraiban is több kiadás és példány található belőlük.
A könyv enciklopédikus jellegű. Foglalkozik az erővel, a hang sebességével, a zenével, az emberi hang csodáival, a fénytöréssel és -visszaverődéssel, a lencsékkel, a szem szerkezetével, a látással, az általános tömegvonzás törvényével, az árapály jelenségével, a lélek és a test viszonyával, a logikával, a lélek halál utáni állapotával, az idealistákkal, a materialistákkal, a lelki és fizikai szenvedésekkel, az ember küldetésével, a bűnösök megtérésével.
Ez a könyv szerzője pedagógiai hozzáértését bizonyítja. Euler mindig szívesen tanította gyerekeit, tanítványait és unokáit. Úgy gondolta, nem tett volna meg mindent a tudományért, ha nem mutatta volna meg azokat az ötleteket, amelyek elvezették őt felfedezéseihez.
Számunkra igen érdekes a 102-108. levél. Euler itt halmazokkal, logikával foglalkozik. Kör formájában már használja az ún. Venn-diagramokat szemléltetésre. Itt is kedveli a táblázatos összefoglalásokat.
A 102. levélben először az általános fogalmakat és az absztrakciókat ismerteti. Megfogalmazza az igenlő és a tagadó állításokat. Minden elméleti tételét példán elemzi. A következő predikátumokhoz tartozó példában A jelenti az embereket, B azt a tulajdonságot, hogy az ember(ek) halandó(k):
Az A ember és a B halandó fogalmakat egy-egy körrel ábrázolja, és segítségükkel szemlélteti az egyes eseteket, majd az eredményeket összefoglaló táblázatba rendezi.
Érdemes megjegyezni, hogy a hercegnőhöz írt Levelek logikai tudnivalói meghaladják a mai középiskolások ismereteinek átlagos szintjét.
Bevezetés az algebrába
Ez a könyv volt Euler másik legnépszerűbb műve. 100 000-es példányszámban jelent meg. A legenda szerint a szerző az íráskor már vak volt, és egy fiatal szabóinasnak diktálta le a könyvet, aki még nem tanult algebrát. Euler a feladatoknak csak a szövegét mondta tollba, a megoldásokat a szabóinasnak kellett elkészítenie. Ez a módszer Euler jó pedagógiai érzékét tükrözte, hiszen ilyen módon ellenőrizni tudta, hogy tanítványa megértette-e az általa diktált algebrát. Igaz viszont, hogy néhány hiba maradt a könyvben. A munka tiszta, világos gondolatmenettel tárja fel az algebrai ismereteket, pontos didaktikai felépítést követ. A legegyszerűbb fogalmakkal, műveletekkel indít, amelyek a kezdő számára feltétlenül szükségesek: (természetes) számok, alapműveletek, elsőfokú, másodfokú, harmadfokú, negyedfokú és diofantikus egyenletek. Mai szemmel nézve a könyv az általános és középiskolai algebrát tartalmazza. A másodfokú egyenletek megoldására kétféle módszert is megad. Mintaszerű a szöveges egyenletek tárgyalása.
Érdekesség, hogy Hatvani István - a törtszámok négyzetre emelésénél - kézírással, latinul kiegészítette Euler táblázatát.
Epilógus
Euler tiszteletére hat alkalommal bocsátottak ki bélyeget. NDK: 1950, 1957, 1983, Szovjetunió: 1957, Svájc: 1957, 2007. A bélyegeken Euler különböző arcképei láthatók, illetve a 250. éves évforduló német és a 300. éves évforduló svájci bélyegén az Euler-féle poliéder-tétel (e - k + f = 2).
Svájcban a 10 frankoson Euler képe látható.
Az Orosz Tudományos Akadémia - a Szteklov Intézet részeként - megalapította a Nemzetközi Euler Matematikai Intézetet (EIMI) a szentpétervári tudományos akadémián. Az intézet 1990-ben kezdte meg működését.
2007-ben, Euler születésének 300. évfordulóján, életének mind a három színterén, Bázelben, Berlinben és Szentpéterváron megemlékezést, konferenciát tartanak, kiállításokat szerveznek és könyveket adnak ki (www.euler-2007.ch, www.bbaw.de, www.pdmi.ras.ru/EIMI).
Euler jelentősége az utókor számára
A svájci megemlékezések kiemelik Euler munkásságának gyakorlati és XXI. századi alkalmazásait:
Matematikai munkái a chipek készítésének alapját képezik.
A prímszámeloszlásnak nagy szerepe van a kódelméletben, az adatátvitelnél (pl. e-bank esetében).
A titkosírási technikában az Euler-féle j -függvényt használják fel (Public Key Exchange).
Fontosak az optikai alkalmazások.
A ballisztika eredményei ma is használhatók és szükségesek (repülőgép- és hajóépítés, variációszámítás alkalmazása).
A merev testek rugalmasságának kérdései aktuálisak például a hídépítésnél, az oszlopok és erkélyek szakítási szilárdságának vizsgálatánál.
A vasúti pályák, autópályák íveinek építésénél a variációszámítást alkalmazzák.
A mesterséges szívbillentyűk kifejlesztésénél is támaszkodtak Euler eredményeire.
Irodalom
_________________________
Természet Világa 2007. szeptember - EULER-EMLÉKÉV (2007)